Деление python: Числа: целые, вещественные, комплексные | Python 3 для начинающих и чайников
Содержание
Числа: целые, вещественные, комплексные | Python 3 для начинающих и чайников
Числа в Python 3: целые, вещественные, комплексные. Работа с числами и операции над ними.
Целые числа (int)
Числа в Python 3 ничем не отличаются от обычных чисел. Они поддерживают набор самых обычных математических операций:
| x + y | Сложение |
| x — y | Вычитание |
| x * y | Умножение |
| x / y | Деление |
| x // y | Получение целой части от деления |
| x % y | Остаток от деления |
| -x | Смена знака числа |
| abs(x) | Модуль числа |
| divmod(x, y) | Пара (x // y, x % y) |
| x ** y | Возведение в степень |
| pow(x, y[, z]) | xy по модулю (если модуль задан) |
Также нужно отметить, что целые числа в python 3, в отличие от многих других языков, поддерживают длинную арифметику (однако, это требует больше памяти). y
y
Дополнительные методы
int.bit_length() — количество бит, необходимых для представления числа в двоичном виде, без учёта знака и лидирующих нулей.
>>> n = -37 >>> bin(n) '-0b100101' >>> n.bit_length() 6
int.to_bytes(length, byteorder, *, signed=False) — возвращает строку байтов, представляющих это число.
>>> (1024).to_bytes(2, byteorder='big') b'\x04\x00' >>> (1024).to_bytes(10, byteorder='big') b'\x00\x00\x00\x00\x00\x00\x00\x00\x04\x00' >>> (-1024).to_bytes(10, byteorder='big', signed=True) b'\xff\xff\xff\xff\xff\xff\xff\xff\xfc\x00' >>> x = 1000 >>> x.to_bytes((x.bit_length() // 8) + 1, byteorder='little') b'\xe8\x03'
classmethod int. from_bytes(bytes, byteorder, *, signed=False) — возвращает число из данной строки байтов.
from_bytes(bytes, byteorder, *, signed=False) — возвращает число из данной строки байтов.
>>> int.from_bytes(b'\x00\x10', byteorder='big') 16 >>> int.from_bytes(b'\x00\x10', byteorder='little') 4096 >>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=True) -1024 >>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=False) 64512 >>> int.from_bytes([255, 0, 0], byteorder='big') 16711680
Системы счисления
Те, у кого в школе была информатика, знают, что числа могут быть представлены не только в десятичной системе счисления. К примеру, в компьютере используется двоичный код, и, к примеру, число 19 в двоичной системе счисления будет выглядеть как 10011. Также иногда нужно переводить числа из одной системы счисления в другую. Python для этого предоставляет несколько функций:
- int([object], [основание системы счисления]) — преобразование к целому числу в десятичной системе счисления. По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.

- bin(x) — преобразование целого числа в двоичную строку.
- hex(х) — преобразование целого числа в шестнадцатеричную строку.
- oct(х) — преобразование целого числа в восьмеричную строку.
Примеры:
>>> a = int('19') # Переводим строку в число
>>> b = int('19.5') # Строка не является целым числом
Traceback (most recent call last):
File "", line 1, in
ValueError: invalid literal for int() with base 10: '19.5'
>>> c = int(19.5) # Применённая к числу с плавающей точкой, отсекает дробную часть
>>> print(a, c)
19 19
>>> bin(19)
'0b10011'
>>> oct(19)
'0o23'
>>> hex(19)
'0x13'
>>> 0b10011 # Так тоже можно записывать числовые константы
19
>>> int('10011', 2)
19
>>> int('0b10011', 2)
19Вещественные числа (float)
Вещественные числа поддерживают те же операции, что и целые. Однако (из-за представления чисел в компьютере) вещественные числа неточны, и это может привести к ошибкам:
>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 0.9999999999999999
Для высокой точности используют другие объекты (например Decimal и Fraction)).
Также вещественные числа не поддерживают длинную арифметику:
>>> a = 3 ** 1000 >>> a + 0.1 Traceback (most recent call last): File "", line 1, in OverflowError: int too large to convert to float
Простенькие примеры работы с числами:
>>> c = 150 >>> d = 12.9 >>> c + d 162.9 >>> p = abs(d - c) # Модуль числа >>> print(p) 137.1 >>> round(p) # Округление 137
Дополнительные методы
float.as_integer_ratio() — пара целых чисел, чьё отношение равно этому числу.
float.is_integer() — является ли значение целым числом.
float.hex() — переводит float в hex (шестнадцатеричную систему счисления).
classmethod float.fromhex(s) — float из шестнадцатеричной строки.
>>> (10.5).hex() '0x1.5000000000000p+3' >>> float.fromhex('0x1.5000000000000p+3') 10.5
Помимо стандартных выражений для работы с числами (а в Python их не так уж и много), в составе Python есть несколько полезных модулей.
Модуль math предоставляет более сложные математические функции.
>>> import math >>> math.pi 3.141592653589793 >>> math.sqrt(85) 9.219544457292887
Модуль random реализует генератор случайных чисел и функции случайного выбора.
>>> import random >>> random.random() 0.15651968855132303
Комплексные числа (complex)
В Python встроены также и комплексные числа:
>>> x = complex(1, 2) >>> print(x) (1+2j) >>> y = complex(3, 4) >>> print(y) (3+4j) >>> z = x + y >>> print(x) (1+2j) >>> print(z) (4+6j) >>> z = x * y >>> print(z) (-5+10j) >>> z = x / y >>> print(z) (0.44+0.08j) >>> print(x.conjugate()) # Сопряжённое число (1-2j) >>> print(x.imag) # Мнимая часть 2.0 >>> print(x.real) # Действительная часть 1.0 >>> print(x > y) # Комплексные числа нельзя сравнить Traceback (most recent call last): File "", line 1, in TypeError: unorderable types: complex() > complex() >>> print(x == y) # Но можно проверить на равенство False >>> abs(3 + 4j) # Модуль комплексного числа 5.0 >>> pow(3 + 4j, 2) # Возведение в степень (-7+24j)
Для работы с комплексными числами используется также модуль cmath.
Python | Операции с числами
Операции с числами
Последнее обновление: 20.06.2017
Арифметические операции
Python поддерживает все распространенные арифметические операции:
+
Сложение двух чисел:
print(6 + 2) # 8
—
Вычитание двух чисел:
print(6 - 2) # 4
*
Умножение двух чисел:
print(6 * 2) # 12
/
Деление двух чисел:
print(6 / 2) # 3.
 0
0//
Целочисленное деление двух чисел:
print(7 / 2) # 3.5 print(7 // 2) # 3
Данная операция возвращает целочисленный результат деления, отбрасывая дробную часть
**
Возведение в степень:
print(6 ** 2) # Возводим число 6 в степень 2. Результат - 36
%
Получение остатка от деления:
print(7 % 2) # Получение остатка от деления числа 7 на 2. Результат - 1
В данном случае ближайшее число к 7, которое делится на 2 без остатка, это 6. Поэтому остаток от деления равен 7 — 6 = 1
При последовательном использовании нескольких арифметических операций их выполнение производится в соответствии с их приоритетом.
В начале выполняются операции с большим приоритетом. Приоритеты операций в порядке убывания приведены в следующей таблице.
Операции | Направление |
** | Справо налево |
* / // % | Слева направо |
+ — | Слева направо |
Пусть у нас выполняется следующее выражение:
number = 3 + 4 * 5 ** 2 + 7 print(number) # 110
Здесь начале выполняется возведение в степень (5 ** 2) как операция с большим приоритетом, далее результат умножается на 4 (25 * 4), затем происходит сложение
(3 + 100) и далее опять идет сложение (103 + 7).
Чтобы переопределить порядок операций, можно использовать скобки:
number = (3 + 4) * (5 ** 2 + 7) print(number) # 224
Следует отметить, что в арифметических операциях могут принимать участие как целые, так и дробные числа. Если в одной операции участвует
целое число (int) и число с плавающей точкой (float),
то целое число приводится к типу float.
Арифметические операции с присвоением
Ряд специальных операций позволяют использовать присвоить результат операции первому операнду:
+=
Присвоение результата сложения
-=
Присвоение результата вычитания
*=
Присвоение результата умножения
/=
Присвоение результата от деления
//=
Присвоение результата целочисленного деления
**=
Присвоение степени числа
%=
Присвоение остатка от деления
Примеры операций:
number = 10 number += 5 print(number) # 15 number -= 3 print(number) # 12 number *= 4 print(number) # 48
Функции преобразования чисел
Ряд встроенных функций в Python позволяют работать с числами. В частности, функции int() и float()
В частности, функции int() и float()
позволяют привести значение к типу int и float соответственно.
Например, пусть у нас будет следующий код:
first_number = "2" second_number = 3 third_number = first_number + second_number
Мы ожидаем, что «2» + 3 будет равно 5. Однако этот код сгенерирует исключение, так как первое число на самом деле представляет строку.
И чтобы все заработало как надо, необходимо привести строку к числу с помощью функции int():
first_number = "2" second_number = 3 third_number = int(first_number) + second_number print(third_number) # 5
Аналогичным образом действует функция float(), которая преобразует в число с плавающей точкой. Но вообще с дробными числами надо учитывать, что результат операций с ними
может быть не совсем точным. Например:
first_number = 2.0001 second_number = 5 third_number = first_number / second_number print(third_number) # 0.40002000000000004
В данном случае мы ожидаем получить число 0.40002, однако в конце через ряд нулей появляется еще какая-то четверка. Или еще одно выражение:
print(2.0001 + 0.1) # 2.1001000000000003
В этот случае для округления результата мы можем использовать функцию round():
first_number = 2.0001 second_number = 0.1 third_number = first_number + second_number print(round(third_number, 4)) # 2.1001
Первый параметр функции — округляемое число, а второй — сколько знаков после запятой должно содержать получаемое число.
Представление числа
При обычном определении числовой переменной она получает значение в десятичной системе. Но кроме десятичной в Python мы можем использовать двоичную,
восьмеричную и шестнадцатеричную системы.
Для определения числа в двоичной системе перед его значением ставится 0 и префикс b:
x = 0b101 # 101 в двоичной системе равно 5
Для определения числа в восьмеричной системе перед его значением ставится 0 и префикс o:
a = 0o11 # 11 в восьмеричной системе равно 9
Для определения числа в шестнадцатеричной системе перед его значением ставится 0 и префикс x:
y = 0x0a # a в шестнадцатеричной системе равно 10
И с числами в других системах измерения также можно проводить арифметические операции:
x = 0b101 # 5
y = 0x0a # 10
z = x + y # 15
print("{0} in binary {0:08b} in hex {0:02x} in octal {0:02o}". format(z))
format(z))
Для вывода числа в различных системах исчисления используются функция format, которая вызывается у строки.
В эту строку передаются различные форматы. Для двоичной системы «{0:08b}», где число 8 указывает, сколько знаков должно быть в записи числа. Если знаков указано больше, чем
требуется для числа, то ненужные позиции заполняются нулями. Для шестнадцатеричной системы применяется формат «{0:02x}». И здесь все аналогично — запись числа состоит из двух знаков, если один знак не нужен, то вместо него вставляется ноль.
А для записи в восьмеричной системе испольуется формат «{0:02o}».
Результат работы скрипта:
15 in binary 00001111 in hex 0f in octal 17
Остаток от деления в Python 3 и целая часть при делении
Python — популярный высокоуровневый язык программирования. Он обладает большим набором инструментов, имеет динамическую типизацию и используется для решения любых видов задач.
Деление в Python разделяется на три вида: обычное, целочисленное и взятие остатка. Программисту не нужно заботиться о типах операндов, Python сам определяет их и приводит результат к нужному виду. Как это делается, разберемся в этой статье.
Программисту не нужно заботиться о типах операндов, Python сам определяет их и приводит результат к нужному виду. Как это делается, разберемся в этой статье.
Оператор деления
Деление в Python обозначается косой чертой «/». Примечательно, что результат в консоле всегда приводится к типу «float», даже если оба операнда были целочисленного типа, об этом свидетельствует появление «.0» у полученного значения.
Это появилось в 3-ей версии Python, ранее результатом деления целых чисел было только целое число, чтобы получить дробный результат, программисты явно указывали одному из операндов тип «float», в противном случае дробная часть просто отбрасывалась.
Важно понимать, что деление в Python, как и другие операции, работает медленнее, чем в более низкоуровневых языках программирования. Это связано с высоким уровнем автоматизации и абстракции, из-за динамической типизации интерпретатор вынужден приводить числа к дробному типу «float», который требует большего количества памяти.
Деление в представлении человека отличается от его представления в компьютере. Компьютер устроен так, что все арифметические операции могут выполняться только через сложение. Это значит, что быстрее всего выполняется сложение, затем вычитание, где необходимо менять знак операндов, умножение, где число складывается много раз. Деление выполняется дольше всех, потому что помимо многократно повторяющейся операции сложения необходимо также менять знак операндов, что требует больше памяти и действий.
Примеры:
print(int(1) / int(2)) print(5 / 5) print(1 / 3) 0.5 1.0 0.3333333333333333
Из примера видно, что не смотря на то, что во всех случаях операция была между целыми числами, результатом деления в Python 3 является вещественное число. В первом случае мы даже специально использовали приведение к типу int.
Дополнительно хотелось бы отметить, что если точности типа данных float не достаточно, можно воспользоваться библиотекой decimal. В частности мы её использовали при написании программы «калькулятор» в отдельной статье.
Деление без остатка
Чтобы выполнить деление на цело в Python, можно воспользоваться целочисленным делением. В этом случае результатом будет целое число, без остатка. Целочисленное деление в Python обозначается двумя косыми чертами «//».
В отличие от других языков программирования Python позволяет результату целочисленного деления быть как целым (int), так и дробным (float) числом. В обоих случаях дробная часть отбрасывается и получается число с окончанием «.0».
Примеры нахождения целой части от деления:
print(5 // 2) print(0 // 2) print(1234 // 5.0) 2 0 246.0
В первых двух случаях деление осуществлялось между целыми числами. Поэтому в результате было получено целое число. В третьем примере одно из чисел вещественное. В этом случае в результате получаем так же вещественное число (типа float), после запятой у которого 0.
Остаток
Для получения остатка от деления в Python 3 используется операция, обозначающаяся символом процента «%». Остаток — это оставшаяся после целочисленного деления часть числа. Операция взятия остатка используется для решения различных видов задач.
Примеры:
print(10 % 3) print(5 % 10) print(5 % 0.25) 1 5 0.0
Определение остатка от деления очень часто используется в программах для нахождения, допустим, чётных чисел. Или, например, если обработка данных выполняется в цикле, и нужно выводить в консоль сообщение о ходе обработки не каждый раз, а на каждой 10-ой итерации.
Вот пример вывода чётных чисел из списка в консоль:
example_list = [3, 7, 2, 8, 1, 12]
for value in example_list:
if value % 2 == 0:
print(value)
2
8
12Проблемы чисел с плавающей точкой
Компьютер устроен так, что на аппаратном уровне понимает только две цифры: один и ноль. Из-за этого при делении и других операциях с дробями часто возникают проблемы. Например, 1/10 в двоичном представлении является неправильной бесконечной дробью. Её нельзя написать полностью, поэтому приходится округлять, а выбор значения при округлении ограничен нулем и единицей.
Что говорить о делении, если ошибки возникают и при операции сложения. Если сложить число «0.1» с самим собой четырнадцать раз, то получиться 1.400…01. Откуда взялась эта единица? Она появилась при переводе числа из двоичного вида в десятичный.
a = 0.1
for i in range(13):
a += 0.1
print(a)
1.4000000000000001Более технически сложное деление приводит к подобным неточностям гораздо чаще. Обычно Python округляет результат так, что пользователь не замечает этой проблемы, но если получается достаточно длинное число, то проблема проявляется.
Деление комплексных чисел
Комплексные числа — это числа вида «a + b·i». Они занимают наивысшую ступень в иерархии чисел, арифметические операции над ними существенно отличаются от операций над обычными числами.
Деление комплексного числа на обычное меняет лишь длину радиус вектора, но не его направление.
Пример:
print((5 + 8j) / 2) (2.5+4j)
Сокращенные операции деления
Чтобы упростить жизнь программистов, разработчики Python включили в язык «сокращенные операции». Их используют если надо выполнить операцию над переменной и полученный результат записать в эту же переменную. То, что записывается в длинной форме, можно записать в более короткой по следующим правилам:
| Полная форма | Краткая форма | |
| Деление | a = a / b | a /= b |
| Целая часть | a = a // b | a //=b |
| Остаток | a = a % b | a %= b |
Приведём пример:
a = 245 a %= 17 print(a) 7
Деление на ноль
Если попробовать в Python выполнить деление на 0, то мы получим исключение ZeroDivisionError.
Исключение следует обрабатывать, это можно сделать так:
try:
print(24 / 0)
except Exception as e:
print(e)
division by zeroНо в этом случае мы обрабатываем все исключения. Зачастую так делать не совсем корректно. Мы знаем, что в нашем коде возможно деление на 0 и, чтобы отловить именно эту ошибку, следует заменить except Exception as e: на except ZeroDivisionError as e:.
Но можно и проверять перед выполнением операции, что делитель не равен 0. Например так:
a = 14
b = None
if a == 0:
print('делитель равен нулю!')
else:
b = 345/a
print('Операция выполнена, результат = ' + str(b))
Операция выполнена, результат = 24.642857142857142Интерактивный учебник языка Python
1. Целочисленная арифметика
Для целых чисел определены операции
+, -, * и **. Операция
деления / для целых чисел возвращает вещественное число (значение типа float).
Также функция возведения в степень возвращает значение типа float,
если показатель степени — отрицательное число.
Но есть и специальная операция целочисленного деления, выполняющегося с отбрасыванием
дробной части, которая обозначается // (она соответствует операции div в Паскале).
Она возвращает целое число: целую часть частного. Другая близкая ей операция − это операция взятия остатка от деления,
обозначаемая % (она соответствует операции mod в Паскале).
Например:
print(17 / 3) # выведет 5.66666666667 print(17 // 3) # выведет 5 print(17 % 3) # выведет 2
2. Действительные числа
В этом разделе речь пойдет о действительных числах, имеющих тип float.
Обратите внимание, что если вы хотите считать с клавиатуры действительное
число, то результат, возращаемый функцией input() необходимо
преобразовывать к типу float:
1.492
x = float(input()) print(x)
Действительные (вещественные) числа представляются в виде чисел с десятичной точкой (а не запятой, как принято
при записи десятичных дробей в русских текстах). Для записи очень больших или очень маленьких
по модулю чисел используется так называемая запись «с плавающей точкой»
(также называемая «научная» запись). В этом случае число представляется в виде
некоторой десятичной дроби, называемой мантиссой, умноженной на целочисленную степень десяти
(порядок). Например, расстояние от Земли
до Солнца равно 1.496·1011, а масса молекулы воды 2.99·10-23.
Числа с плавающей точкой в программах на языке Питон, а также при вводе и выводе записываются так:
сначала пишется мантисса, затем пишется буква e, затем пишется порядок. Пробелы внутри этой
записи не ставятся. Например, указанные выше константы можно записать в виде
1.496e11 и 2.99e-23. Перед самим числом также может стоять знак минус.
Напомним, что результатом операции деления / всегда является действительное число (float),
в то время как результатом операции // является целое число (int).
Преобразование действительных чисел к целому производится с округлением
в сторону нуля, то есть int(1.7) == 1, int(-1.7) == -1.
3. Библиотека math
Для проведения вычислений с действительными числами язык Питон содержит много
дополнительных функций, собранных в библиотеку (модуль), которая называется math.
Для использования этих функций в начале программы необходимо подключить математическую
библиотеку, что делается командой
import math
Например, пусть мы хотим округлять вещественные числа до ближайшего целого числа вверх.
Соответствующая функция ceil от одного аргумента вызывается, например, так: math.ceil(x)
(то есть явно указывается, что из модуля math используется функция ceil).
Вместо числа x может быть любое число, переменная или выражение.
Функция возращает значение, которое можно вывести на экран, присвоить
другой переменной или использовать в выражении:
import math x = math.ceil(4.2) y = math.ceil(4.8) print(x) print(y)
Другой способ использовать функции из библиотеки math, при котором не нужно будет
при каждом использовании функции из модуля math указывать название
этого модуля, выглядит так:
from math import ceil x = 7 / 2 y = ceil(x) print(y)
или так:
from math import * x = 7 / 2 y = ceil(x) print(y)
Ниже приведен список основных функций модуля math. Более подробное описание
этих функций можно найти на сайте с документацией языка Питон.
Некоторые из перечисленных функций (int, round, abs)
являются стандартными и не требуют подключения модуля math для использования.
| Функция | Описание |
|---|---|
| Округление | |
int(x) | Округляет число в сторону нуля. Это стандартная функция, для ее использования не нужно подключать модуль math. |
round(x) | Округляет число до ближайшего целого. Если дробная часть числа равна 0.5, то число округляется до ближайшего четного числа. |
round(x, n) | Округляет число xдо n знаков после точки. Это стандартная функция, для ее использования не нужно подключатьмодуль math. |
floor(x) | Округляет число вниз («пол»), при этом floor(1.5) == 1, floor(-1.5) == -2 |
ceil(x) | Округляет число вверх («потолок»), при этом ceil(1.5) == 2, ceil(-1.5) == -1 |
abs(x) | Модуль (абсолютная величина). Это — стандартная функция. |
| Корни, логарифмы | |
sqrt(x) | Квадратный корень. Использование: sqrt(x) |
log(x) | Натуральный логарифм. При вызове в виде log(x, b) возвращает логарифм по основанию b. |
e | Основание натуральных логарифмов e = 2,71828… |
| Тригонометрия | sin(x) | Синус угла, задаваемого в радианах |
cos(x) | Косинус угла, задаваемого в радианах |
tan(x) | Тангенс угла, задаваемого в радианах |
asin(x) | Арксинус, возвращает значение в радианах |
acos(x) | Арккосинус, возвращает значение в радианах |
atan(x) | Арктангенс, возвращает значение в радианах |
atan2(y, x) | Полярный угол (в радианах) точки с координатами (x, y). |
degrees(x) | Преобразует угол, заданный в радианах, в градусы. |
radians(x) | Преобразует угол, заданный в градусах, в радианы. |
pi | Константа π = 3.1415… |
Ссылки на задачи доступны в меню слева. Эталонные решения теперь доступны на странице самой задачи.
Язык программирования «Python». Деление нацело и деление по остатку
Условие
задачи
На вход программе поступает натуральное значение бит. Программа переводит это значение в запись типа:
«x1 Тбайт х2 Гбайт х3 Мбайт х4 Кбайт х5 байт х6 бит».
| № | Входные данные | Выходные данные |
|---|---|---|
| 1 | Введите число бит: 1050 | 0 Тбайт 0 Гбайт 0 Мбайт 1 Кбайт 3 байт 2 бит |
Изучаем Python: математические операции
В этом руководстве мы будем работать с двумя типами данных в Python – целыми числами (integer) и числами с плавающей точкой (floats):
- Целые – числа без дробной части, которые могут быть положительными, отрицательными или нулём (…, -1, 0, 1, …).
- С плавающей точкой – это числа, содержащие десятичную точку (например, 9.0 или -2.25).
В этой статье будут описаны операции с числовыми типами данных в Python.
Оператор – это символ, которая обозначает операцию. Например, в математике знак плюса или + – это оператор сложения.
Мы рассмотрим схожие операторы, которые перешли в Python из математики. Но другие операторы специфичны именно для программирования.
Ниже представлена таблица с кратким обзором математических операторов, доступных в Python.
| Операция | Возвращаемое значение |
| x + y | Сумма x и y. |
| x — y | Разность x и y. |
| -x | Изменение знака x. |
| +x | Тождественность x. |
| x * y | Произведение x и y. |
| x / y | Частное от деления x на y. |
| x // y | Частное от целочисленного деления x на y. |
| x % y | Остаток от деления x / y. |
| x ** y | x в степени y. |
В Python операторы суммы и разности выполняют те же операции, что и в математике. Поэтому вы можете использовать этот язык программирования как калькулятор.
Рассмотрим некоторые примеры. Начнём с целых чисел:
Вывод
Вместо передачи целых чисел напрямую в функцию print мы можем инициализировать переменные для этих значений:
a = 88 b = 103 print(a + b)
Вывод
Целые числа могут быть как положительными, так и отрицательными. Поэтому можно добавлять отрицательные числа к положительным:
c = -36 d = 25 print(c + d)
Вывод
Прибавление работает аналогично и с числами с плавающей запятой:
e = 5.5 f = 2.5 print(e + f)
Вывод
Синтаксис разности тот же, что и для прибавления, за исключением того, что вместо оператора сложения (+) необходимо использовать оператор вычитания (-):
g = 75.67 h = 32 print(g - h)
Вывод
В этом примере мы вычитаем целое число из числа с плавающей точкой. Python возвратит число с плавающей точкой, если хотя бы одно из чисел выражения является числом с плавающей точкой.
Унарное математическое выражение состоит из одного элемента. Знаки плюса и минуса в питоне могут быть использованы как единичный оператор, чтобы вернуть тождественное значение (+) или сменить знак числа (-).
Знак плюса означает тождественное значение. Мы можем использовать его с положительными значениями:
Вывод
Когда мы используем знак плюса с отрицательным значением, он также вернёт значение тождественное данному. В этом случае он вернёт отрицательное значение:
Вывод
При использовании с отрицательным значением знак плюса возвращает то же отрицательное значение.
Минус (в отличие от знака плюса) изменяет знак числа. Поэтому при передаче положительного числа мы получим отрицательное значение:
Вывод
А когда мы используем минус в качестве унарного оператора с отрицательным значением, будет возвращено положительное число:
Вывод
Унарные арифметические операторы возвращают тождественное значение в случае с +i, или противоположное по знаку число в случае с -i.
Оператор, которые мы будем использовать в Python для умножения «*», а для деления «/». Пример умножения двух чисел с плавающей точкой в Python:
k = 100.1 l = 10.1 print(k * l)
Вывод
Когда вы выполняете деление в Python 3, частное всегда будет числом с плавающей точкой, даже если вы используете два целых числа:
m = 80 n = 5 print(m / n)
Вывод
Это одно из наиболее существенных отличий Python 2 от Python 3. В Python 3 результатом будет дробное число. Поэтому, когда вы используете оператора «/» для деления 11 на 2, возвращено будет 5.5. В Python 2 возвращаемое значение деления 11 / 2 было 5.
В Python 2 оператор «/» выполняет целочисленное деление, где частное x, а возвращаемое число – это наибольшее целое число, меньшее или равное x. Если вы выполните пример, приведённый выше, в Python 2, то получите 16 без десятичной точки.
Целочисленное деление python 3 использует оператор «//». Выражение 100 // 40 вернёт значение 2.
Оператор % используется для деления по модулю, и возвращает остаток от деления, а не частное. Это полезно, например, для нахождения множителей числа.
Деление по модулю Python (с остатком) — пример:
o = 85 p = 15 print(o % p)
Вывод
В этом примере 85 делится на 15. Результат – 5 с остатком 10. Значение 10 выводится, поскольку оператор возвращает остаток от деления.
Если мы используем два числа с плавающей точкой для деления по модулю, число с плавающей точкой будет возвращено в качестве остатка:
q = 36.0 r = 6.0 print(o % p)
Вывод
В приведенном выше примере 36.0 делится на 6.0 без остатка, поэтому возвращается значение 0.0.
Оператор «**» в Python используется для возведения числа, расположенного слева от оператора в степень, указанную справа. То есть, в выражении 5 ** 3, число 5 возводится в третью степень.
В математике часто используется выражение 5³. То есть 5 умножается на себя три раза. В Python мы получим тот же результат (125) выполнив 5 ** 3 или 5 * 5 * 5.
Пример с переменными:
s = 52.25 t = 7 print(s ** t) 1063173305051.292
Возведение числа с плавающей точкой 52.25 в степень 7 с помощью оператора ** приводит к выводу большого числа с плавающей точкой.
Операторы Python выполняются в порядке приоритета. Посмотрим на следующее выражение:
Умножение выполняется первым. Поэтому, если мы вызовем метод print(u), то получим следующее значение:
Вывод
Это потому, что 10 * 5 равно 50, а затем мы прибавляем 10, чтобы получить 60.
Если нужно было сложить 10 и 10, и умножить сумму на 5, то пришлось бы использовать скобки, как в математике:
u = (10 + 10) * 5 print(u)
Вывод
Оператор «=» присваивает значение, расположенное справа, переменной слева. Например, v = 23 присваивает значение числа 23 переменной v.
В программировании часто используют составные операторы присваивания. Они соединяют арифметический оператор с оператором «=». Поэтому для сложения мы используем оператор «+» с оператором «=», чтобы получить составной оператор «+=». Пример:
Вывод
Сначала мы задаём переменной w значение 5. Затем используем составной оператор присваивания +=, чтобы прибавить число справа, к переменной, расположенной слева, и присвоить результат переменной w.
Составные операторы присваивания часто используются в циклах for:
for x in range (0, 7):
x *= 2
print(x)Вывод
При помощи for можно автоматизировать процесс использования оператора «*=». Он умножает переменную w на число 2, а затем присваивает полученный результат переменной w для следующей итерации цикла.
В Python предусмотрен составной оператор присваивания для каждой арифметической операции:
y += 1 # добавить число и присвоить результат y -= 1 # отнять число и присвоить результат y *= 2 # умножить на число и присвоить результат y /= 3 # разделить на число и присвоить результат y // = 5 # разделить без остатка на число и присвоить результат y **= 2 # возвести в степень и присвоить результат y %= 3 # вернуть остаток от деления и присвоить результат
Составные операторы присваивания полезны в тех случаях, когда переменная должна увеличиваться или уменьшаться с помощью инкремента. А также когда необходимо автоматизировать некоторый процесс в создаваемой программе.
В этой статье рассмотрены операторы, которые используются для математических операций с целыми и дробными десятичными числами.
Данная публикация является переводом статьи «How To Do Math in Python 3 with Operators» , подготовленная редакцией проекта.
Деление с остатком преподнесло сюрприз
Деление с остатком – часто используемая операция в программировании. Начиная от классических заданий для начинающих на вычисление минут и секунд:
total_seconds = 119
seconds = total_seconds % 60
minutes = total_seconds // 60
print(f'{minutes}:{seconds}') # 1:59Заканчивая тем, что на остатках построена львиная доля криптографии. Нахождения остатка часто называют modulo (или коротко mod).
При делении a на b неполное частное q и остаток r связаны формулой:
a = b · q + r, где b ≠ 0
В Python 3 частное и остаток вычисляются операторами:
q = a // b r = a % b
Именно двойной слэш, одинарный слэш – деление без остатка (до конца). Иногда двойной слэш называют целочисленным делением, что не очень справедливо, потому что мы можем без проблем делить числа с запятой. Если оба числа целые (int), то частное будет тоже целым числом (int), иначе float. Посмотрите примеры:
10 / 3 == 3.3333333333333335 10 // 3 == 3 10.0 / 3.0 == 3.3333333333333335 10.0 // 3.0 == 3.0 10.0 % 3.0 == 1.0 10 % 3 == 1 2.4 // 0.4 == 5.0 2.4 / 0.4 == 5.999999999999999 2.4 % 0.4 == 0.3999999999999998
Последние три примера немного обескураживают из-за особенностей вычислений с плавающей точкой на компьютере, но формула a = b · q + r всегда остается справедлива.
Поговорим об отрицательных числах. Математически остаток не должен быть меньше нуля и больше или равен модулю делителя b: 0 ≤ r < |b|. Однако, Intel в своих процессорах случайно либо намеренно ввела отрицательные остатки в реализации ассемблерных команд деления. Компиляторы языков C и С++, являясь платформо-зависимыми, обычно полагаются на процессорное поведение. Пример на С++. И вообще посмотрите на эту огромную таблицу, каждый язык программирования пляшет, как хочет. Не будем спорить, кто из них прав. Просто узнаем, как у нас в Python:
a, b = [10, -10], [3, -3]
for x in a:
for y in b:
print(f'{x} // {y} = {x // y}')
print(f'{x} % {y} = {x % y}')
print()
10 // 3 = 3
10 % 3 = 1
10 // -3 = -4
10 % -3 = -2
-10 // 3 = -4
-10 % 3 = 2
-10 // -3 = 3
-10 % -3 = -1Формула выполняется всегда, но результаты отличаются для С++ и Python, где при делении на положительное число – остаток всегда положителен, а на отрицательное число – отрицателен. Если бы мы сами реализовали взятие остатка, то получилось бы так:
def mod_python(a, b): return int(a - math.floor(a / b) * b) # на С++ работает так: def mod_cpp(a, b): return int(a - math.trunc(a / b) * b)
Где floor – ближайшее целое число не превышающее аргумент: floor(-3.3) = -4, а trunc – функция отбрасывания целой части: trunc(-3.3) = -3. Разница проявляется между ними только для отрицательных чисел. Отсюда и разные остатки и частные – все зависит от того, с какой стороны числовой оси мы приближаемся к частному.
Вывод: если вам доведется писать или портировать код, где возможно деление отрицательных чисел с остатком, будьте предельно аккуратны, и помните про разницу поведения деления в разных языках.
🐉 Специально для канала @pyway. Подписывайтесь на мой канал в Телеграм @pyway 👈
2 353
Python — Операторы подразделений
Как правило, тип данных выражения зависит от типов
аргументы. Это правило соответствует нашим ожиданиям для большинства операторов: когда
складываем два целых числа, результат должен быть целым. Однако это
не подходит для деления, потому что есть два разных
ожидания. Иногда мы ожидаем, что разделение даст точные ответы,
обычно эквиваленты дробей с плавающей запятой. В других случаях мы хотим
округленный целочисленный результат.
Классическое определение Python / полностью зависит от
по аргументам.685/252 было 2, потому что оба аргумента были целыми числами.
Однако 685./252. было 2,7182539682539684, потому что аргументы
плавающая запятая.
Это определение часто вызывало проблемы для приложений, в которых
были использованы типы, которых автор не ожидал. Например, простой
программа, конвертирующая градусы Цельсия в градусы Фаренгейта, будет производить разные
ответы в зависимости от ввода. Если один пользователь предоставляет 18, а другой
дает 18.0, ответы были разными, хотя все входные
все имели одинаковые числовые значения.
>>>печать 18 * 9/5 + 3264>>>печать 18,0 * 9/5 + 3264,4>>>18 == 18,0Правда>>>
Эта неожиданная неточность обычно связана с случайным использованием
целые числа, для которых числа с плавающей запятой были более подходящими. (Это может
также встречаются с использованием целых чисел, где неявно ожидались комплексные числа.)
Явная функция преобразования (например,
с плавающей запятой (
х
)) может помочь предотвратить это.
Идея, однако, состоит в том, чтобы Python был простым и разреженным языком, без
плотный беспорядок конверсий, чтобы скрыть редкий случай неожиданного
тип данных.
Начиная с Python 2.2, в
уточнить, чего ожидалось. Обычный оператор / через
будущее, возвращать результаты с плавающей запятой. Оператор специального подразделения,
// , вернет результаты с округлением в меньшую сторону.Как правило, новый
Оператор / — это то, что будет выполнять большинство математических вычислений.
использовать.
Дополнительно были сделаны доступными два инструмента, которые заканчиваются
Python 3.0. Эти инструменты позволят оператору подразделения, /,
работать либо по старым (классическим, до версии 2.2) правилам, либо
новые правила. Это дает программистам возможность сохранять старые приложения
Бег; это также дает им возможность явно объявить, что программа
использует более новое определение оператора. Это состоит из двух частей:
statememt, который можно разместить в программе, а также в командной строке
параметр, который можно использовать при запуске интерпретатора Python.
Программные положения. Чтобы упростить переход от старых языковых функций к новым,
доступен модуль __future__ . Этот
модуль включает определение раздела , которое
изменяет определение оператора / с классического на
будущее. Вы можете включить следующие
из
утверждение
заявить, что ваша программа зависит от будущего определения
разделение.
из отдела импорта __future__ печать 18 * 9/5 + 32 печать 18 * 9 // 5 + 32
Это дает следующий результат.Первая строка показывает новое использование
оператора / для получения результатов с плавающей запятой, даже если
оба аргумента являются целыми числами. Вторая строка показывает //
оператор, который округляет результаты в меньшую сторону.
64,4 64
от __future__
заявление установит
ожидание того, что ваш скрипт использует деление с плавающей запятой нового стиля
оператор. Это позволяет вам начинать писать программы с версии 2.2, которые
будет корректно работать со всеми будущими версиями.В версии 3.0 этот импорт
заявление больше не будет необходимо, и их нужно будет удалить
из нескольких модулей, которые их использовали.
Программистам стоит поставить
от __future__
в каждом файле сценария Python, чтобы убедиться, что они
запись будет работать правильно. В конце концов, их можно удалить, но для
в обозримом будущем они являются необходимой частью каждого скрипта Python
файл.
Параметры командной строки. Еще один инструмент для облегчения перехода — это параметр командной строки.
при запуске интерпретатора Python.Это может заставить старый стиль
интерпретация оператора / или предупредить о старом стиле
использование оператора / между целыми числами. Это также может заставить
новый стиль использования оператора / и отчет обо всех
потенциально неправильное использование оператора /.
Параметр командной строки интерпретатора Python -Q будет
принудительно обработать оператор / классическим образом
(«Старый») или с будущей («новой») семантикой.
Если вы запустите Python с -Qold , оператор /
результат зависит от аргументов.Если вы запускаете Python с
-Qnew , результат оператора / будет плавающим
точка. В любом случае оператор // возвращает округленное значение в меньшую сторону.
целочисленный результат.
Вы можете использовать -Qold , чтобы заставить старые модули и программы
работают с версией 2.2 и выше. Однако когда будет выпущен Python 3.0,
этот переход больше не будет поддерживаться; к тому времени у вас уже должно быть
исправили ваши программы и модули.
Чтобы упростить исправление, параметр командной строки -Q может
возьмите два других значения: warnall и warnall .если ты
используйте -Qwarn , затем оператор / применяется к
целочисленные аргументы генерируют предупреждение во время выполнения. Это позволит вам
найти и исправить ситуации, когда оператор // может быть больше
соответствующий. Если вы используете -Qwarnall , то все экземпляры
Оператор / генерирует предупреждение; это подарит вам близость
посмотрите свои программы.
Вы можете включить параметр командной строки при запуске Python
устный переводчик. Для пользователей Linux и MacOS вы также можете поместить это на
#! Строка в начале файла сценария.
#! / Usr / local / bin / python -Qnew
Оператор по модулю Python — что означает символ% в Python? (Решено)
Когда вы видите символ%, вы можете подумать «процент». Но в Python, как и в большинстве других языков программирования, это означает нечто иное.
Символ % в Python называется оператором по модулю. Он возвращает остаток от деления левого операнда на правый операнд. Он используется для получения остатка от задачи деления.
Оператор по модулю считается арифметической операцией вместе с + , - , /, * , ** , // .
Базовый синтаксис:
a% b В предыдущем примере a делится на b , а остаток возвращается. Давайте посмотрим на пример с числами.
7% 2 Результат предыдущего примера — один .Два переходит в семь три раза, и остается , один .
На диаграмме ниже показано визуальное представление 7/2 и 7% 2 («R» означает «остаток»). Единственный логотип справа (с указывающей на него зеленой стрелкой) — это остаток от проблемы разделения. Это также ответ на 7% 2 .
Вот еще один пример:
3% 4 В результате получится три .Четыре не входит в три ни один раз, поэтому исходный три все еще остается. На схеме ниже показано, что происходит. Помните, что оператор по модулю возвращает остаток после выполнения деления. Остаток — три.
Пример использования оператора по модулю
Одним из распространенных способов использования оператора по модулю является поиск четных или нечетных чисел. В приведенном ниже коде оператор по модулю используется для печати всех нечетных чисел от 0 до 10.
для числа в диапазоне (1, 10):
если (число% 2! = 0):
печать (число) Результат:
1
3
5
7
9 В чем причина разницы между целочисленным делением и преобразованием float в int в Python?
Последовательность.— Обратите внимание, что число перед. это int (x / 4)
До этого момента вы могли полагать, что x // 4 и int (x / 4) всегда дают одинаковый результат. Это ваше нынешнее понимание ситуации.
Однако посмотрите, что происходит при целочисленном делении: число за R циклически изменяется с 3, 2, 1 до 0, а затем снова начинается: 3, 2, 1, 0. Число перед R уменьшается с каждым 4-м шагом.
Итак, как это будет продолжаться?
8 ÷ 4 = 2 R 0
7 ÷ 4 = 1 р 3
6 ÷ 4 = 1 К 2
5 ÷ 4 = 1 р 1
4 ÷ 4 = 1 R 0
3 ÷ 4 = 0 R 3
2 ÷ 4 = 0 R 2
1 ÷ 4 = 0 R 1
0 ÷ 4 = 0 R 0
-1 ÷ 4 = -1 R 3
^ ------ Нам нужно убавиться сейчас, потому что у нас уже 0 четыре раза
^ - Мы должны перезапустить цикл на 3
В то же время деление вещественных чисел дает нам:
-1 ÷ 4 = -0.----- Перед.
Вот почему -1 // 4 дает -1, а int (-1/4) дает 0.
Есть ли мотивация для различий между функциями?
Ну, они служат для разных целей: // — это часть целочисленного вычисления с остатками, а int () дает вам часть перед . операции с действительным числом.
Вы решаете, что хотите вычислить, а затем решаете, какой оператор использовать в Python для получения правильного результата.
Хороший вопрос. Продолжайте учиться.
/ (деление) оператор — ArcGIS Pro | Документация
Доступно с лицензией Spatial Analyst.
Доступно с лицензией Image Analyst.
Обсуждение
При использовании оператора с растровым вводом результатом будет растр. Однако, если все входные данные являются числами, результатом будет число.
Когда в выражении используется несколько операторов, они не обязательно выполняются в порядке слева направо.Оператор с наивысшим значением приоритета будет выполнен первым. Дополнительные сведения о приоритете операторов см. В таблице приоритетов операторов. Вы можете использовать круглые скобки для управления порядком выполнения.
Порядок ввода актуален для этого оператора.
Когда число делится на ноль, результатом является NoData.
Точная техника деления, используемая этим оператором, зависит от приложения, которое используется при его выполнении.
В ArcGIS Pro для этого оператора всегда используется деление с плавающей запятой Python 3, и на выходе всегда будет значение с плавающей запятой.Например, если 3 разделить на 2, получится 1,5.
В ArcMap оператор деления использует технику целочисленного деления Python 2, при которой сохраняется только целое частное. Если оба ввода являются целыми числами, оператор выполняет целочисленное деление, и на выходе получается целое число. Например, если 3 делится на 2, на выходе получается 1, а если -3 делится на 2, на выходе получается -2. Если любой из входных данных имеет тип с плавающей запятой, оператор деления выполняет деление с плавающей запятой, и на выходе будет значение с плавающей запятой.Например, если 3 разделить на 2,0, получится 1,5.
Помните об этом различии, если вы переходите с ArcGIS Desktop на ArcGIS Pro или будете работать в смешанной среде обоих. Вы можете использовать оператор // (Целочисленное деление), если важно сохранить целочисленный вывод.
Другой способ выполнить операцию деления — a / = b, что является альтернативным способом записи a = a / b.
Если оба входа являются одноканальными растрами или один из входных данных является константой, на выходе будет одноканальный растр.
Если оба входа являются многополосными растрами или один из входных данных является постоянным, на выходе будет многополосный растр. Количество полос на каждом многополосном входе должно быть одинаковым.
Оператор будет выполнять операцию на каждом диапазоне с одного входа по отношению к соответствующему диапазону с другого входа. Если один из входных данных является многополосным растром, а другой вход является постоянным, оператор выполнит операцию с постоянным значением для каждой полосы в многополосном входе.
Как использовать оператор% — Real Python
Python поддерживает широкий спектр арифметических операторов, которые вы можете использовать при работе с числами в вашем коде. Одним из этих операторов является оператор по модулю (% ), который возвращает остаток от деления двух чисел.
Оператор по модулю Python иногда может быть упущен из виду. Но хорошее понимание этого оператора даст вам бесценный инструмент в вашем арсенале инструментов Python.
Математический модуль по модулю
Термин по модулю происходит от раздела математики, называемого модульной арифметикой.Модульная арифметика имеет дело с арифметикой целых чисел на круговой числовой строке с фиксированным набором чисел. Все арифметические операции, выполняемые на этой числовой строке, будут повторяться, когда они достигнут определенного числа, называемого модулем модуля .
Классический пример модульной арифметики — это двенадцатичасовые часы. Двенадцатичасовые часы имеют фиксированный набор значений от 1 до 12. При подсчете двенадцатичасовых часов вы рассчитываете до модуля 12, а затем возвращаетесь к 1. Двенадцатичасовые часы можно классифицировать как « по модулю 12 », иногда сокращается до« по модулю 12.”
Оператор по модулю используется, когда вы хотите сравнить число с модулем и получить эквивалентное число, ограниченное диапазоном модуля.
Например, скажем, вы хотите определить, сколько времени будет через девять часов после 8:00. В двенадцатичасовом формате вы не можете просто прибавить 9 к 8, потому что вы получите 17. Вам нужно взять результат, 17, и используйте mod , чтобы получить эквивалентное значение в двенадцатичасовом контексте:
8 часов + 9 = 17 часов
17 мод 12 = 5
17 mod 12 возвращает 5 .Это означает, что девять часов после 8:00 — это 17:00. Вы определили это, взяв число 17 и применив его к контексту mod 12 .
Теперь, если подумать, 17 и 5 эквивалентны в контексте mod 12 . Если бы вы посмотрели на часовую стрелку в 5:00 и 17:00, она была бы в том же положении. В модульной арифметике есть уравнение, описывающее эту взаимосвязь:
Это уравнение гласит: « a и b равны по модулю n .Это означает, что a и b эквивалентны в mod n , поскольку они имеют одинаковый остаток при делении на n . В приведенном выше уравнении n — это модуль для a и b . Используя значения 17 и 5 из предыдущих, уравнение будет выглядеть так:
Это гласит: « 17 и 5 равны по модулю 12 ». 17 и 5 имеют одинаковый остаток, 5 , при делении на 12 .Таким образом, в mod 12 числа 17 и 5 эквивалентны.
Подтвердить это можно с помощью деления:
17/12 = 1 К 5
5/12 = 0 R 5
Обе операции имеют одинаковый остаток, 5 , поэтому они эквивалентны по модулю 12 .
Теперь это может показаться сложным математическим делом для оператора Python, но эти знания подготовят вас к использованию оператора по модулю в примерах далее в этом руководстве.В следующем разделе вы познакомитесь с основами использования оператора Python по модулю с числовыми типами int и float .
Основы операторов Python по модулю
Оператор по модулю, как и другие арифметические операторы, может использоваться с числовыми типами int и float . Как вы увидите позже, его также можно использовать с другими типами, такими как math.fmod () , decimal.Decimal и вашими собственными классами.
Оператор по модулю с
int
В большинстве случаев вы будете использовать оператор по модулю с целыми числами.Оператор по модулю, когда он используется с двумя положительными целыми числами, вернет остаток от стандартного евклидова деления:
>>>
>>> 15% 4
3
>>> 17% 12
5
>>> 240% 13
6
>>> 10% 16
10
Будьте осторожны! Как и в случае с оператором деления (/), Python вернет ZeroDivisionError , если вы попытаетесь использовать оператор по модулю с делителем 0 :
>>>
>>> 22% 0
ZeroDivisionError: целочисленное деление или по модулю нуля
Далее вы познакомитесь с использованием оператора по модулю с числом с плавающей запятой .
Оператор по модулю с поплавком
Подобно int , оператор по модулю, используемый с числом с плавающей запятой , вернет остаток от деления, но как значение с плавающей запятой :
>>>
>>> 12,5% 5,5
1.5
>>> 17,0% 12,0
5.0
Альтернативой использованию с плавающей запятой с оператором по модулю является использование math.fmod () для выполнения операций по модулю над с плавающей запятой значений:
>>>
>>> импорт математики
>>> математика.fmod (12.5, 5.5)
1.5
>>> math.fmod (8.5, 2.5)
1.0
Официальные документы Python предлагают использовать math.fmod () вместо оператора Python modulo при работе со значениями float , поскольку math.fmod () вычисляет результат операции по модулю. Если вы используете отрицательный операнд, вы можете увидеть разные результаты между math.fmod (x, y) и x% y . В следующем разделе вы более подробно исследуете использование оператора по модулю с отрицательными операндами.
Как и другие арифметические операторы, оператор по модулю и math.fmod () могут столкнуться с проблемами округления и точности при работе с арифметикой с плавающей запятой:
>>>
>>> 13,3% 1,1
0,09999999999999964
>>> импорт математики
>>> math.fmod (13.3, 1.1)
0,09999999999999964
Если для вашего приложения важно поддерживать точность с плавающей запятой, вы можете использовать оператор по модулю с десятичным числом .Десятичный . Вы рассмотрите это позже в этом руководстве.
Оператор по модулю с отрицательным операндом
Все операции по модулю, которые вы видели до этого момента, использовали два положительных операнда и возвращали предсказуемые результаты. Когда вводится отрицательный операнд, все становится сложнее.
Как оказалось, способ, которым компьютеры определяют результат операции по модулю с отрицательным операндом, оставляет неоднозначность относительно того, должен ли остаток принимать знак делимого (число, которое делится) или знак делителя (число, на которое делится дивиденд).Разные языки программирования обрабатывают это по-разному.
Например, в JavaScript остаток примет знак делимого:
Остаток в этом примере, 2 , положительный, поскольку принимает знак дивиденда 8 . В Python и других языках остаток примет знак делителя:
Здесь вы можете видеть, что остаток -1 принимает знак делителя -3 .
Вам может быть интересно, почему остаток в JavaScript равен 2 , а остаток в Python равен -1 .Это связано с тем, как разные языки определяют результат операции по модулю. Языки, в которых остаток принимает знак делимого, используют следующее уравнение для определения остатка:
В этом уравнении есть три переменные:
-
r— остаток. -
a— дивиденды. -
n— делитель.
trunc () в этом уравнении означает, что используется усеченное деление , которое всегда округляет отрицательное число до нуля.Для получения дополнительной информации см. Шаги операции по модулю ниже, используя 8 в качестве делимого и -3 в качестве делителя:
r = 8 - (-3 * усечение (8 / -3))
r = 8 - (-3 * усечение (-2,666666666667))
r = 8 - (-3 * -2) # Округление в сторону 0
г = 8 - 6
г = 2
Здесь вы можете увидеть, как такой язык, как JavaScript, получает остаток 2 . Python и другие языки, в которых остаток принимает знак делителя, используют следующее уравнение:
этаж () в этом уравнении означает, что используется разделение этажа .При положительных числах деление этажа вернет тот же результат, что и усеченное деление. Но при отрицательном числе деление по этажам округляет результат в меньшую сторону, в сторону от нуля:
r = 8 - (-3 * этаж (8 / -3))
r = 8 - (-3 * этаж (-2.666666666667))
r = 8 - (-3 * -3) # Округление от 0
г = 8 - 9
г = -1
Здесь видно, что результат -1 .
Теперь, когда вы понимаете, откуда берется разница в остатке, вам может быть интересно, почему это важно, если вы используете только Python.Как оказалось, не все операции по модулю в Python одинаковы. В то время как модуль, используемый с типами int и float , принимает знак делителя, другие типы — нет.
Вы можете увидеть пример этого, сравнив результаты 8.0% -3.0 и math.fmod (8.0, -3.0) :
>>>
>>> 8.0% -3
-1,0
>>> импорт математики
>>> math.fmod (8.0, -3.0)
2.0
математ.fmod () принимает знак делимого с использованием усеченного деления, тогда как float использует знак делителя. Позже в этом руководстве вы увидите другой тип Python, в котором используется знак делимого, десятичное . Десятичное .
Оператор по модулю и
divmod ()
Python имеет встроенную функцию divmod () , которая внутренне использует оператор по модулю. divmod () принимает два параметра и возвращает кортеж, содержащий результаты деления по этажам и по модулю с использованием предоставленных параметров.
Ниже приведен пример использования divmod () с 37 и 5 :
>>>
>>> divmod (37, 5)
(7, 2)
>>> 37 // 5
7
>>> 37% 5
2
Вы можете видеть, что divmod (37, 5) возвращает кортеж (7, 2) . 7 является результатом разделения этажей на 37 и 5 . 2 является результатом 37 по модулю 5 .
Ниже приведен пример, в котором второй параметр представляет собой отрицательное число. Как обсуждалось в предыдущем разделе, когда оператор по модулю используется с int , остаток примет знак делителя:
>>>
>>> divmod (37, -5)
(-8, -3)
>>> 37 // -5
-8
>>> 37% -5
-3 # Результат имеет знак делителя
Теперь, когда у вас была возможность увидеть оператор по модулю, используемый в нескольких сценариях, важно взглянуть на то, как Python определяет приоритет оператора по модулю при использовании с другими арифметическими операторами.
Приоритет оператора по модулю
Как и другие операторы Python, для оператора по модулю существуют особые правила, определяющие его приоритет при вычислении выражений. Оператор по модулю (% ) имеет тот же уровень приоритета, что и операторы умножения ( * ), деления (/) и деления пола ( // ).
Взгляните на пример приоритета оператора по модулю ниже:
>>>
>>> 4 * 10% 12 - 9
-5
Операторы умножения и по модулю имеют одинаковый уровень приоритета, поэтому Python будет оценивать их слева направо.Вот шаги для вышеуказанной операции:
-
4 * 10оценивается, в результате получается40% 12 - 9. -
40% 12оценивается, в результате получается4 - 9. -
4 - 9вычисляется, в результате получается-5.
Если вы хотите переопределить приоритет других операторов, вы можете заключить в круглые скобки операцию, которую вы хотите вычислить первой:
>>>
>>> 4 * 10% (12 - 9)
1
В этом примере сначала оценивается (12–9) , затем 4 * 10 и, наконец, 40% 3 , что равно 1 .
Оператор модуля Python на практике
Теперь, когда вы познакомились с основами оператора Python по модулю, вы рассмотрите несколько примеров его использования для решения реальных задач программирования. Иногда бывает трудно определить, когда использовать в коде оператор по модулю. Приведенные ниже примеры дадут вам представление о многих способах его использования.
Как проверить, четное или нечетное число
В этом разделе вы увидите, как можно использовать оператор по модулю, чтобы определить, является ли число четным или нечетным.Используя оператор по модулю с модулем 2 , вы можете проверить любое число, чтобы увидеть, делится ли оно без остатка на 2 . Если оно делится без остатка, то это четное число.
Взгляните на is_even () , который проверяет, является ли параметр num четным:
def is_even (число):
вернуть число% 2 == 0
Здесь num% 2 будет равно 0 , если num четное, и 1 , если num нечетное.Проверка против 0 вернет логическое значение True или False в зависимости от того, является ли num четным.
Проверка на нечетные числа очень похожа. Чтобы проверить нечетное число, вы инвертируете проверку равенства:
def is_odd (число):
вернуть число% 2! = 0
Эта функция вернет True , если num% 2 не равно 0 , что означает, что остаток доказывает, что num — нечетное число.Теперь вам может быть интересно, можно ли использовать следующую функцию, чтобы определить, является ли num нечетным числом:
def is_odd (число):
вернуть число% 2 == 1
Ответ на этот вопрос — да и нет. Технически эта функция будет работать так же, как Python вычисляет по модулю с целыми числами. Тем не менее, вам следует избегать сравнения результата операции по модулю с 1 , поскольку не все операции по модулю в Python будут возвращать тот же остаток.
Вы можете понять, почему, на следующих примерах:
>>>
>>> -3% 2
1
>>> 3% -2
-1
Во втором примере остаток принимает знак отрицательного делителя и возвращает -1 . В этом случае логическая проверка 3% -2 == 1 вернет False .
Однако, если вы сравните операцию по модулю с 0 , то не имеет значения, какой операнд отрицательный. Результатом всегда будет Истинно , когда это четное число:
.
>>>
>>> -2% 2
0
>>> 2% -2
0
Если вы будете сравнивать операцию Python по модулю с 0 , то у вас не должно возникнуть проблем с проверкой четных и нечетных чисел или любых других кратных чисел в вашем коде.
В следующем разделе вы узнаете, как можно использовать оператор по модулю с циклами для управления потоком вашей программы.
Как запускать код с определенными интервалами в цикле
С помощью оператора модуля Python вы можете запускать код через определенные промежутки времени внутри цикла. Это делается путем выполнения операции по модулю с текущим индексом цикла и модулем. Номер модуля определяет, как часто код, зависящий от интервала, будет выполняться в цикле. 15}», end = «»)
если индекс% модуля == 0:
Распечатать()
Распечатать()
Этот код определяет split_names_into_rows () , который принимает два параметра. name_list — это список имен, который следует разбить на строки. модуль устанавливает модуль для операции, эффективно определяя, сколько имен должно быть в каждой строке. split_names_into_rows () будет перебирать name_list и начинать новую строку после достижения значения модуля .
Прежде чем разбирать функцию более подробно, взгляните на нее в действии:
>>>
>>> names = ["Пикард", "Райкер", "Трой", "Крашер", "Ворф", "Дейта", "Ла Форж"]
>>> split_names_into_rows (имена)
---- Пикард ----- ----- Райкер ----- ----- Трой ------
---- Дробилка ---- ----- Worf ------ ----- Данные ------
--- Ла Форж ----
Как видите, список имен разделен на три строки, максимум по три имени в каждой строке.Модуль по умолчанию 3 , но вы можете указать любое число:
>>>
>>> split_names_into_rows (имена, модуль = 4)
---- Пикард ----- ----- Райкер ----- ----- Трой ------ ---- Крашер ----
----- Ворф ------ ----- Данные ------ --- Ла Форж ----
>>> split_names_into_rows (имена, модуль = 2)
---- Пикард ----- ----- Райкер -----
----- Трой ------ ---- Дробилка ----
----- Worf ------ ----- Данные ------
--- Ла Форж ----
>>> split_names_into_rows (имена, модуль = 1)
---- Пикард -----
----- Райкер -----
----- Трой ------
----Дробилка----
----- Ворф ------
-----Данные------
--- Ла Форж ----
Теперь, когда вы увидели код в действии, вы можете разобрать, что он делает.Во-первых, он использует enumerate () для перебора name_list , присваивая текущий элемент в списке name и значение счетчика index . Вы можете видеть, что необязательный аргумент start для enumerate () имеет значение 1 . Это означает, что счетчик индекса начнется с 1 вместо 0 :
.
для индекса, имя в перечислении (name_list, start = 1):
Затем внутри цикла функция вызывает print () для вывода name в текущую строку.15 Синтаксис сообщает print () следующее:
- Выведите не менее
15символов, даже если строка короче 15 символов. - Выровняйте строку по центру.
- Заполните любое пространство справа или слева от строки символом дефиса (
–).
Теперь, когда имя напечатано в строке, взглянем на основную часть split_names_into_rows () :
, если индекс% модуля == 0:
Распечатать()
Этот код берет индекс текущей итерации и, используя оператор по модулю, сравнивает его с модулем .Если результат равен 0 , то он может запустить код, зависящий от интервала. В этом случае функция вызывает print () , чтобы добавить новую строку, которая начинает новую строку.
Приведенный выше код является только одним примером. Использование шаблона index% modulus == 0 позволяет вам запускать другой код через определенные промежутки времени в ваших циклах. В следующем разделе вы немного углубитесь в эту концепцию и рассмотрите циклическую итерацию.
Как создать циклическую итерацию
Циклическая итерация описывает тип итерации, которая сбрасывается при достижении определенной точки.Как правило, этот тип итерации используется для ограничения индекса итерации определенным диапазоном.
Вы можете использовать оператор по модулю для создания циклической итерации. Взгляните на пример использования библиотеки turtle для рисования формы:
импортная черепаха
случайный импорт
def draw_with_cyclic_iteration ():
colors = ["зеленый", "голубой", "оранжевый", "фиолетовый", "красный", "желтый", "белый"]
turtle.bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.выбор (цвета)) # Первый цвет случайный
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
turtle.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
В приведенном выше коде используется бесконечный цикл для рисования повторяющейся формы звезды. После каждых шести итераций он меняет цвет пера. Размер пера увеличивается с каждой итерацией, пока i не будет сброшено обратно на 0 .Если запустить код, то должно получиться что-то вроде этого:
Важные части этого кода выделены ниже:
импортная черепаха
случайный импорт
def draw_with_cyclic_iteration ():
colors = ["зеленый", "голубой", "оранжевый", "фиолетовый", "красный", "желтый", "белый"]
turtle.bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.choice (цвета))
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
черепаха.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
Каждый раз при прохождении цикла i обновляется на основе результатов (i + 1)% 6 . Это новое значение i используется для увеличения . Компенсация с каждой итерацией. Как только i достигнет 5 , (i + 1)% 6 будет равно 0 , а i вернется к 0 .
Вы можете увидеть шаги итерации ниже для более ясного понимания:
я = 0: (0 + 1)% 6 = 1
я = 1: (1 + 1)% 6 = 2
я = 2: (2 + 1)% 6 = 3
я = 3: (3 + 1)% 6 = 4
я = 4: (4 + 1)% 6 = 5
i = 5: (5 + 1)% 6 = 0 # Сброс
Когда i сбрасывается обратно на 0 , .pencolor изменяется на новый случайный цвет, как показано ниже:
, если i == 0:
turtle.pencolor (random.choice (цвета))
Код в этом разделе использует 6 в качестве модуля, но вы можете установить его на любое число, чтобы настроить, сколько раз цикл будет повторяться перед сбросом значения i .
Как преобразовать единицы
В этом разделе вы узнаете, как использовать оператор по модулю для преобразования единиц. В следующих примерах единицы меньшего размера преобразуются в единицы большего размера без использования десятичных знаков. Оператор по модулю используется для определения любого остатка, который может существовать, когда меньшая единица не делится без остатка на большую единицу.
В этом первом примере вы преобразуете дюймы в футы. Оператор по модулю используется для получения оставшихся дюймов, которые неравномерно не делятся на футы.Оператор деления пола ( // ) используется для округления общего количества футов в меньшую сторону:
def convert_inches_to_feet (total_inches):
дюймы = total_inches% 12
футов = total_inches // 12
print (f "{total_inches} дюймов = {футов} футов и {дюймов} дюймов")
Вот пример используемой функции:
>>>
>>> convert_inches_to_feet (450)
450 дюймов = 37 футов и 6 дюймов
Как видно из выходных данных, 450% 12 возвращает 6 , то есть оставшиеся дюймы, которые не были равномерно разделены на футы.Результатом 450 // 12 является 37 , что представляет собой общее количество футов, на которое дюймы были равномерно разделены.
В следующем примере вы можете пойти немного дальше. convert_minutes_to_days () принимает целое число, total_mins , представляющее количество минут, и выводит период времени в днях, часах и минутах:
def convert_minutes_to_days (total_mins):
дней = total_mins // 1440
extra_minutes = total_mins% 1440
часы = extra_minutes // 60
минут = дополнительные_минуты% 60
print (f "{total_mins} = {дней} дней, {часов} часов и {минут} минут")
Разбив это, вы можете увидеть, что функция выполняет следующие функции:
- Определяет общее количество равномерно делимых дней с
total_mins // 1440, где1440- количество минут в дне - Вычисляет любые
дополнительных_минутоставшихся сtotal_mins% 1440 - Использует
дополнительных_минутдля получения равномерно делимыхчасови любых дополнительныхминут
Вы можете увидеть, как это работает, ниже:
>>>
>>> convert_minutes_to_days (1503)
1503 = 1 день, 1 час и 3 минуты
>>> convert_minutes_to_days (3456)
3456 = 2 дня, 9 часов и 36 минут
>>> convert_minutes_to_days (35000)
35000 = 24 дня, 7 часов и 20 минут
В то время как приведенные выше примеры относятся только к преобразованию дюймов в футы и минут в дни, вы можете использовать любой тип единиц с оператором по модулю, чтобы преобразовать меньшую единицу в большую единицу.
Примечание : Оба приведенных выше примера можно изменить для использования divmod () , чтобы сделать код более лаконичным. Если вы помните, divmod () возвращает кортеж, содержащий результаты деления этажа и по модулю с использованием предоставленных параметров.
Ниже операторы деления этажа и модуля были заменены на divmod () :
def convert_inches_to_feet_updated (total_inches):
футы, дюймы = divmod (total_inches, 12)
print (f "{total_inches} дюймов = {футов} футов и {дюймов} дюймов")
Как видите, divmod (total_inches, 12) возвращает кортеж, который распаковывается в футов и дюймов .
Если вы попробуете эту обновленную функцию, то получите те же результаты, что и раньше:
>>>
>>> convert_inches_to_feet (450)
450 дюймов = 37 футов и 6 дюймов
>>> convert_inches_to_feet_updated (450)
450 дюймов = 37 футов и 6 дюймов
Вы получите тот же результат, но теперь код более лаконичный. Вы также можете обновить convert_minutes_to_days () :
def convert_minutes_to_days_updated (total_mins):
дней, extra_minutes = divmod (total_mins, 1440)
часы, минуты = divmod (extra_minutes, 60)
print (f "{total_mins} = {дней} дней, {часов} часов и {минут} минут")
При использовании divmod () функция легче читается, чем предыдущая версия, и возвращает тот же результат:
>>>
>>> convert_minutes_to_days (1503)
1503 = 1 день, 1 час и 3 минуты
>>> convert_minutes_to_days_updated (1503)
1503 = 1 день, 1 час и 3 минуты
Использование divmod () не обязательно для всех ситуаций, но здесь имеет смысл, поскольку при расчетах преобразования единиц используется как деление по этажам, так и по модулю.
Теперь, когда вы узнали, как использовать оператор по модулю для преобразования единиц, в следующем разделе вы узнаете, как можно использовать оператор по модулю для проверки простых чисел.
Как определить, является ли число простым числом
В следующем примере вы посмотрите, как можно использовать оператор Python по модулю, чтобы проверить, является ли число простым числом . Простое число - это любое число, которое содержит только два множителя: 1 и само себя. Некоторые примеры простых чисел: 2 , 3 , 5 , 7 , 23 , 29 , 59 , 83 и 97 .
Код ниже представляет собой реализацию для определения простоты числа с помощью оператора по модулю:
def check_prime_number (число):
если число <2:
print (f "{число} должно быть больше или равно 2, чтобы быть простым.")
возвращаться
факторы = [(1, число)]
я = 2
в то время как я * я <= число:
если num% i == 0:
Factors.append ((i, num // i))
я + = 1
если len (факторы)> 1:
print (f "{число} не простое число. Имеет следующие множители: {факторы}")
еще:
print (f "{num} - простое число")
Этот код определяет check_prime_number () , который принимает параметр num и проверяет, является ли это простым числом.Если это так, то отображается сообщение о том, что num - простое число. Если это не простое число, отображается сообщение со всеми множителями числа.
Примечание: Приведенный выше код не самый эффективный способ проверки простых чисел. Если вы хотите копнуть глубже, посмотрите на Сито Эратосфена и Сито Аткина, где можно найти примеры более эффективных алгоритмов поиска простых чисел.
Прежде чем вы внимательно посмотрите на функцию, вот результаты с использованием некоторых других чисел:
>>>
>>> check_prime_number (44)
44 не простое.Он имеет следующие факторы: [(1, 44), (2, 22), (4, 11)]
>>> check_prime_number (53)
53 - простое число
>>> check_prime_number (115)
115 не простое. Он имеет следующие факторы: [(1, 115), (5, 23)]
>>> check_prime_number (997)
997 - простое число
Углубившись в код, вы увидите, что он начинается с проверки, меньше ли num 2 . Простые числа могут быть не более 2 . Если число меньше 2 , то выполнение функции не требуется.Он будет print () сообщение и вернет :
, если число <2:
print (f "{число} должно быть больше или равно 2, чтобы быть простым.")
возвращаться
Если num больше 2 , то функция проверяет, является ли num простым числом. Чтобы проверить это, функция перебирает все числа от 2 до квадратного корня из num , чтобы увидеть, делятся ли они на num равномерно. Если одно из чисел делится равномерно, значит, был найден множитель, и num не может быть простым числом.
Вот основная часть функции:
факторов = [(1, число)]
я = 2
в то время как я * я <= число:
если num% i == 0:
Factors.append ((i, num // i))
я + = 1
Здесь есть что распаковать, так что давайте рассмотрим это шаг за шагом.
Сначала создается список из факторов с начальными коэффициентами (1, число) . Этот список будет использоваться для хранения любых других найденных факторов:
Затем, начиная с 2 , код увеличивается на i , пока не достигнет квадратного корня из num .На каждой итерации он сравнивает num с i , чтобы увидеть, делится ли оно без остатка. Коду нужно только проверить квадратный корень из число включительно, потому что он не будет содержать никаких множителей выше этого:
я = 2
в то время как я * я <= число:
если num% i == 0:
Factors.append ((i, num // i))
я + = 1
Вместо того, чтобы пытаться определить квадратный корень из num , функция использует цикл while , чтобы проверить, не является ли i * i <= num .Пока i * i <= num , цикл не достиг квадратного корня из num .
Внутри цикла while оператор по модулю проверяет, делится ли num без остатка на i :
факторов = [(1, число)]
i = 2 # Начать начальный индекс с 2
в то время как я * я <= число:
если num% i == 0:
Factors.append ((i, num // i))
я + = 1
Если число делится без остатка на i , то i является множителем число , и кортеж множителей добавляется к списку множителей .
После завершения цикла и код проверяет, были ли найдены какие-либо дополнительные факторы:
, если len (факторы)> 1:
print (f "{число} не простое число. Имеет следующие множители: {факторы}")
еще:
print (f "{num} - простое число")
Если в списке факторов существует более одного кортежа, то num не может быть простым числом. Для непростых чисел коэффициенты распечатываются. Для простых чисел функция выводит сообщение о том, что num - простое число.
Как реализовать шифры
Оператор модуля Python может использоваться для создания шифров. Шифр - это тип алгоритма для выполнения шифрования и дешифрования входных данных, обычно текста. В этом разделе вы познакомитесь с двумя шифрами: шифром Цезаря и шифром Виженера .
Цезарь Шифр
Первый шифр, на который вы посмотрите, - это шифр Цезаря, названный в честь Юлия Цезаря, который использовал его для тайной передачи сообщений.Это шифр подстановки, который использует подстановку букв для шифрования строки текста.
Шифр Цезаря работает, взяв зашифровываемую букву и сдвинув ее на определенное количество позиций влево или вправо в алфавите. Какая бы буква ни была в этой позиции, используется как зашифрованный символ. Это же значение сдвига применяется ко всем символам в строке.
Например, если сдвиг был 5 , то A сместился бы на пять букв вверх и стал бы F , B стал бы G и так далее.Ниже вы можете увидеть процесс шифрования текста REALPYTHON со сдвигом 5 :
В результате получается шифр WJFQUDYMTS .
Расшифровка шифра выполняется реверсированием сдвига. Процессы шифрования и дешифрования можно описать следующими выражениями, где char_index - это индекс символа в алфавите:
encrypted_char_index = (char_index + shift)% 26
decrypted_char_index = (char_index - сдвиг)% 26
Этот шифр использует оператор по модулю, чтобы гарантировать, что при сдвиге буквы индекс будет перебираться, если будет достигнут конец алфавита.Теперь, когда вы знаете, как работает этот шифр, взгляните на его реализацию:
строка импорта
def caesar_cipher (текст, сдвиг, дешифрование = False):
если не text.isascii () или не text.isalpha ():
Raise ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
верхний регистр = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
индекс = верхний регистр.индекс (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
Этот код определяет функцию с именем caesar_cipher () , которая имеет два обязательных параметра и один необязательный параметр:
-
текст- это текст, который нужно зашифровать или расшифровать. -
сдвиг- количество позиций для сдвига каждой буквы. -
decrypt- это логическое значение, которое задает, нужно ли расшифровыватьtext.
decrypt включен, чтобы можно было использовать одну функцию для обработки как шифрования, так и дешифрования. Эта реализация может обрабатывать только буквенные символы, поэтому функция сначала проверяет, является ли текст буквенным символом в кодировке ASCII:
def caesar_cipher (text, shift, decrypt = False):
если не text.isascii () или не text.isalpha ():
Raise ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
Затем функция определяет три переменные для хранения строчных символов ASCII, прописных символов ASCII и результатов шифрования или дешифрования:
нижний регистр = строка.ascii_lowercase # "abcdefghijklmnopqrstuvwxyz"
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результат = ""
Затем, если функция используется для дешифрования текста , она умножает shift на -1 , чтобы сдвинуть назад:
если расшифровать:
сдвиг = сдвиг * -1
Наконец, caesar_cipher () перебирает отдельные символы в тексте и выполняет следующие действия для каждого символа :
- Проверьте, является ли
charстрочными или прописными буквами. - Получить индекс
charв спискахстрочныхилипрописныхASCII. - Добавьте сдвиг
- Используйте
% 26, чтобы убедиться, что сдвиг вернется к началу алфавита. - Добавить зашифрованный символ к строке результата
После того, как цикл завершает итерацию по значению текста , возвращается результат :
для символов в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = uppercase.index (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
Вот еще раз полный код:
строка импорта
def caesar_cipher (текст, сдвиг, дешифрование = False):
если не text.isascii () или не text.isalpha ():
Raise ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
прописные буквы = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = uppercase.index (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
Теперь запустите код в Python REPL, используя текст meetMeAtOurHideOutAtTwo со сдвигом 10 :
>>>
>>> caesar_cipher ("meetMeAtOurHideOutAtTwo", 10)
woodWoKdYebRsnoYedKdDgy
Зашифрованный результат: woodWoKdYebRsnoYedKdDgy .Используя этот зашифрованный текст, вы можете запустить расшифровку, чтобы получить исходный текст:
>>>
>>> caesar_cipher ("woodWoKdYebRsnoYedKdDgy", 10, decrypt = True)
MeetMeAtOurHideOutAtTwo
Шифр Цезаря - забавное занятие для введения в криптографию. Хотя шифр Цезаря редко используется сам по себе, он является основой для более сложных подстановочных шифров. В следующем разделе вы познакомитесь с одним из потомков шифра Цезаря, шифром Виженера.
Шифр Виженера
Шифр Виженера представляет собой полиалфавитный шифр замещения. Для шифрования он использует разные шифры Цезаря для каждой буквы входящего текста. Шифр Виженера использует ключевое слово, чтобы определить, какой шифр Цезаря следует использовать для поиска буквы шифра.
Вы можете увидеть пример процесса шифрования на следующем изображении. В этом примере вводимый текст REALPYTHON зашифрован с использованием ключевого слова MODULO :
.
Для каждой буквы входящего текста, REALPYTHON , используется буква из ключевого слова MODULO , чтобы определить, какой столбец шифра Цезаря следует выбрать.Если ключевое слово короче вводимого текста, как в случае с MODULO , то буквы ключевого слова повторяются до тех пор, пока все буквы вводимого текста не будут зашифрованы.
Ниже представлена реализация шифра Виженера. Как вы увидите, оператор по модулю используется в функции дважды:
строка импорта
def vigenere_cipher (текст, ключ, decrypt = False):
если не text.isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, символ в перечислении (текст):
current_key = ключ [i% len (ключ)]
char_index = uppercase.index (символ)
key_index = uppercase.index (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
результаты + = верхний регистр [индекс% 26]
вернуть результаты
Вы могли заметить, что подпись для vigenere_cipher () очень похожа на caesar_cipher () из предыдущего раздела:
def vigenere_cipher (текст, ключ, decrypt = False):
если не текст.isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
верхний регистр = строка.ascii_uppercase
результаты = ""
Основное отличие состоит в том, что вместо параметра shift , vigenere_cipher () принимает параметр key , который является ключевым словом, используемым во время шифрования и дешифрования. Еще одно отличие - добавление text.isupper () . На основе этой реализации vigenere_cipher () может принимать только вводимый текст в верхнем регистре.
Подобно caesar_cipher () , vigenere_cipher () выполняет итерацию по каждой букве входного текста, чтобы зашифровать или расшифровать его:
для i, символ в перечислении (текст):
current_key = ключ [i% len (ключ)]
В приведенном выше коде вы можете увидеть, как функция впервые использовала оператор по модулю:
current_key = ключ [i% len (ключ)]
Здесь значение current_key определяется на основе индекса, возвращенного из i% len (key) .Этот индекс используется для выбора буквы из строки ключа , например M из MODULO .
Оператор по модулю позволяет использовать ключевое слово любой длины независимо от длины шифруемого текста . Как только индекс i , индекс символа, который в настоящее время шифруется, равен длине ключевого слова, он начнется с начала ключевого слова.
Для каждой буквы входящего текста несколько шагов определяют, как ее зашифровать или расшифровать:
- Определите
char_indexна основе индексаcharвнутрипрописных букв. - Определите
key_indexна основе индексаcurrent_keyвнутрив верхнем регистре. - Используйте
char_indexиkey_index, чтобы получить индекс для зашифрованного или дешифрованного символа.
Взгляните на эти шаги в приведенном ниже коде:
char_index = верхний регистр.индекс (символ)
key_index = uppercase.index (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
Как видите, индексы для расшифровки и шифрования рассчитываются по-разному.Поэтому в этой функции используется decrypt . Таким образом, вы можете использовать эту функцию как для шифрования, так и для дешифрования.
После определения индекса вы обнаружите, что функция использует второй оператор по модулю:
результатов + = верхний регистр [индекс% 26]
index% 26 гарантирует, что index символа не превышает 25 , таким образом гарантируя, что он остается внутри алфавита. С помощью этого индекса зашифрованный или дешифрованный символ выбирается из прописных и добавляется к результатам .
Вот еще раз полный код шифра Виженера:
строка импорта
def vigenere_cipher (текст, ключ, decrypt = False):
если не text.isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, символ в перечислении (текст):
current_key = ключ [i% len (ключ)]
char_index = uppercase.index (символ)
key_index = прописные буквы.индекс (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
результаты + = верхний регистр [индекс% 26]
вернуть результаты
Теперь запустите его в Python REPL:
>>>
>>> vigenere_cipher (text = "REALPYTHON", key = "MODULO")
DSDFAMFVRH
>>> encrypted = vigenere_cipher (text = "REALPYTHON", key = "MODULO")
>>> печать (в зашифрованном виде)
DSDFAMFVRH
>>> vigenere_cipher (зашифровано, "MODULO", decrypt = True)
РЕАЛПИТОН
Отлично! Теперь у вас есть рабочий шифр Виженера для шифрования текстовых строк.
Расширенное использование оператора по модулю Python
В этом последнем разделе вы поднимете свои знания об операторах по модулю на новый уровень, используя их с десятичным числом . Десятичное число . Вы также узнаете, как добавить .__ mod __ () к своим пользовательским классам, чтобы их можно было использовать с оператором по модулю.
Использование оператора Python по модулю с десятичным числом
. Десятичное число
Ранее в этом руководстве вы видели, как можно использовать оператор по модулю с числовыми типами, такими как int и float , а также с math.fmod () . Вы также можете использовать оператор по модулю с Decimal из модуля decimal . Используйте десятичное число . Десятичное число используется, когда требуется дискретное управление точностью арифметических операций с плавающей запятой.
Вот несколько примеров использования целых чисел с десятичным числом , десятичным числом и оператором по модулю:
>>>
>>> импортировать десятичный
>>> десятичное.Десятичное (15)% десятичное.Десятичное (4)
Десятичный ('3')
>>> десятичный.Десятичный (240)% десятичный. Десятичный (13)
Десятичный ('6')
Вот некоторые числа с плавающей запятой, используемые с десятичным числом . Десятичное число и оператор по модулю:
>>>
>>> decimal.Decimal ("12,5")% decimal.Decimal ("5,5")
Десятичный ('1,5')
>>> decimal.Decimal ("13.3")% decimal.Decimal ("1.1")
Десятичный ('0,1')
Все операции по модулю с десятичным числом . Десятичное число возвращает те же результаты, что и другие числовые типы, за исключением случаев, когда один из операндов является отрицательным.В отличие от int и float , но как и math.fmod () , decimal. Decimal использует знак делимого для результатов.
Взгляните на приведенные ниже примеры, в которых сравниваются результаты использования оператора по модулю со стандартными значениями int и с плавающей запятой и с десятичным числом . Десятичное :
>>>
>>> -17% 3
1 # Знак делителя
>>> десятичное.Десятичное (-17)% десятичное.Десятичное (3)
Десятичный (-2) # Знак дивиденда
>>> 17% -3
-1 # Знак делителя
>>> десятичный.Десятичный (17)% десятичный. Десятичный (-3)
Десятичный ("2") # Знак дивиденда
>>> -13,3% 1,1
1.0000000000000004 # Знак делителя
>>> decimal.Decimal ("- 13,3")% decimal.Decimal ("1,1")
Десятичный ("- 0,1") # Знак дивиденда
По сравнению с math.fmod () , десятичное. Десятичное число будет иметь тот же знак, но точность будет другой:
>>>
>>> decimal.Decimal ("- 13,3")% decimal.Decimal ("1,1")
Десятичный ("- 0,1")
>>> математика.fmod (-13,3, 1,1)
-0,09999999999999964
Как видно из приведенных выше примеров, работа с десятичным числом , десятичным числом и оператором по модулю аналогична работе с другими числовыми типами. Вам просто нужно иметь в виду, как он определяет знак результата при работе с отрицательным операндом.
В следующем разделе вы узнаете, как можно переопределить оператор по модулю в своих классах, чтобы настроить его поведение.
Использование оператора Python Modulo с настраиваемыми классами
Модель данных Python позволяет вам переопределить встроенные методы в объекте Python, чтобы настроить его поведение.В этом разделе вы узнаете, как переопределить .__ mod __ () , чтобы можно было использовать оператор по модулю со своими собственными классами.
В этом примере вы будете работать с классом Студент . Этот класс будет отслеживать количество времени, которое студент учился. Вот начальный номер . Студент класса:
.
класс Студент:
def __init __ (я, имя):
self.name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
себя.study_sessions + = сеансы
Класс Student инициализируется параметром name и начинается с пустого списка study_sessions , который будет содержать список целых чисел, представляющих количество минут, изученных за сеанс. Также существует .add_study_sessions () , который принимает параметр sessions , который должен быть списком учебных сессий, который нужно добавить к study_sessions .
Теперь, если вы помните из приведенного выше раздела о преобразовании единиц, convert_minutes_to_day () использовал оператор Python по модулю для преобразования total_mins в дни, часы и минуты.Теперь вы реализуете модифицированную версию этого метода, чтобы увидеть, как можно использовать свой собственный класс с оператором по модулю:
def total_study_time_in_hours (студент, всего_мин.):
часы = total_mins // 60
минут = total_mins% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
Эту функцию можно использовать с классом Студент для отображения общего количества часов, которые изучил Студент . В сочетании с классом Student , приведенным выше, код будет выглядеть следующим образом:
класс Студент:
def __init __ (я, имя):
себя.name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def total_study_time_in_hours (студент, total_mins):
часы = total_mins // 60
минут = total_mins% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
Если вы загрузите этот модуль в Python REPL, то можете использовать его так:
>>>
>>> jane = Студент ("Джейн")
>>> jane.add_study_sessions ([120, 30, 56, 260, 130, 25, 75])
>>> total_mins = сумма (джейн.study_sessions)
>>> total_study_time_in_hours (Джейн, total_mins)
Джейн занималась 11 часов 36 минут
Приведенный выше код распечатывает общее количество часов, изученных Джейн . Эта версия кода работает, но требует дополнительного шага суммирования study_sessions , чтобы получить total_mins перед вызовом total_study_time_in_hours () .
Вот как можно изменить класс Student , чтобы упростить код:
класс Студент:
def __init __ (я, имя):
себя.name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (сам, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
Переопределив .__ mod __ () и .__ floordiv __ () , вы можете использовать экземпляр Student с оператором по модулю. Вычисление суммы () из study_sessions также входит в класс Student .
С этими изменениями вы можете использовать экземпляр Student непосредственно в total_study_time_in_hours () . Поскольку total_mins больше не требуется, вы можете удалить его:
def total_study_time_in_hours (студент):
часы = студент // 60
минут = студент% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
Вот полный код после изменений:
класс Студент:
def __init __ (я, имя):
себя.name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (сам, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
def total_study_time_in_hours (студент):
часы = студент // 60
минут = студент% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
Теперь, вызвав код в Python REPL, вы увидите, что он гораздо лаконичнее:
>>>
>>> jane = Студент ("Джейн")
>>> Джейн.add_study_sessions ([120, 30, 56, 260, 130, 25, 75])
>>> total_study_time_in_hours (Джейн)
Джейн занималась 11 часов 36 минут
Переопределив .__ mod __ () , вы позволяете своим пользовательским классам вести себя больше, чем встроенные числовые типы Python.
Заключение
На первый взгляд, оператор по модулю Python может не привлечь ваше внимание. Тем не менее, как вы видели, в этом скромном операторе есть так много всего. От проверки четных чисел до шифрования текста - вы видели множество различных применений оператора по модулю.
Из этого руководства вы узнали, как:
- Используйте оператор по модулю с
int,float,math.fmod (),divmod ()иdecimal. Decimal - Вычислить результаты операции по модулю
- Решите реальных проблем с помощью оператора по модулю
- Переопределить
.__ mod __ ()в ваших собственных классах, чтобы использовать их с оператором по модулю
Обладая знаниями, полученными в этом руководстве, теперь вы можете с большим успехом начать использовать оператор по модулю в своем собственном коде.Удачного питонинга!
Как делать математику в Python 3 с операторами
Введение
Числа чрезвычайно распространены в программировании. Они используются для представления таких вещей, как размер экрана, географическое положение, деньги и очки, количество времени, которое проходит в видео, положение игровых аватаров и цвета посредством присвоения числовых кодов.
Умение эффективно выполнять математические операции в программировании - важный навык, который нужно развивать, потому что вам придется часто работать с числами.Хотя понимание математики на высоком уровне, безусловно, может помочь вам стать лучшим программистом, это не является обязательным условием. Если у вас нет математического образования, попробуйте рассматривать математику как инструмент для достижения того, чего вы хотите достичь, и как способ улучшить свое логическое мышление.
Мы будем работать с двумя наиболее часто используемыми числовыми типами данных Python, целыми числами и с плавающей запятой :
- Целые числа - это целые числа, которые могут быть положительными, отрицательными или 0 (…,
-1,0,1,…). - Float - это действительные числа, они содержат десятичную точку (как в
9.0или-2.25).
В этом руководстве будут рассмотрены операторы, которые можно использовать с числовыми типами данных в Python.
Операторы
Оператор - это символ или функция, обозначающая операцию. Например, в математике знак плюс или + - это оператор, обозначающий сложение.
В Python мы увидим некоторые знакомые операторы, перенесенные из математики, но другие операторы, которые мы будем использовать, специфичны для компьютерного программирования.
Вот краткая справочная таблица математических операторов в Python. В этом руководстве мы рассмотрим все следующие операции.
| Эксплуатация | Что возвращает |
|---|---|
| х + у | Сумма x и y |
| х - у | Разница x и y |
| -х | Изменен знак x |
| + x | Идентификационный номер x |
| х * у | Произведение x и y |
| х / у | Частное от x и y |
| х // у | Коэффициент от деления этажа x и y |
| x% y | Остаток от х / у |
| х ** у | x до y мощность |
Мы также рассмотрим составные операторы присваивания, включая + = и * = , которые объединяют арифметический оператор с оператором = .
Сложение и вычитание
В Python операторы сложения и вычитания работают так же, как и в математике. Фактически, вы можете использовать язык программирования Python в качестве калькулятора.
Давайте рассмотрим несколько примеров, начиная с целых чисел:
печать (1 + 5)
Выход
6
Вместо того, чтобы передавать целые числа непосредственно в оператор print , мы можем инициализировать переменные для обозначения целочисленных значений:
а = 88
b = 103
печать (a + b)
Выход
191
Поскольку целые числа могут быть как положительными, так и отрицательными (а также 0), мы можем добавить отрицательное число к положительному числу:
с = -36
d = 25
печать (c + d)
Выход
-11
Сложение будет вести себя аналогично с числами с плавающей запятой:
е = 5.5
f = 2,5
печать (e + f)
Выход
8,0
Поскольку мы сложили два числа с плавающей запятой вместе, Python вернул значение с плавающей запятой с десятичным разрядом.
Синтаксис вычитания такой же, как и для сложения, за исключением того, что вы измените свой оператор со знака плюс ( + ) на знак минус (–):
г = 75,67
в = 32
печать (г - ч)
Выход
43,67
Здесь мы вычли целое число из числа с плавающей запятой.Python вернет число с плавающей запятой, если хотя бы одно из чисел, участвующих в уравнении, является числом с плавающей запятой.
Унарные арифметические операции
Унарное математическое выражение состоит только из одного компонента или элемента, а в Python знаки плюс и минус могут использоваться как один элемент в паре со значением, чтобы вернуть идентичность значения ( + ) или изменить знак значения. ( - ).
Знак плюс, хотя и не используется обычно, указывает на идентичность значения.Мы можем использовать знак плюса с положительными значениями:
я = 3,3
печать (+ я)
Выход
3,3
Когда мы используем знак плюса с отрицательным значением, он также возвращает идентичность этого значения, и в этом случае это будет отрицательное значение:
Дж = -19
печать (+ j)
Выход
-19
При отрицательном значении знак «плюс» возвращает то же отрицательное значение.
Знак минус также меняет знак значения.Итак, когда мы передаем положительное значение, мы обнаруживаем, что знак минус перед значением возвращает отрицательное значение:
я = 3,3
печать (-i)
Выход
-3,3
В качестве альтернативы, когда мы используем унарный оператор знака минус с отрицательным значением, будет возвращено положительное значение:
Дж = -19
печать (-j)
Выход
19
Унарные арифметические операции, обозначенные знаком плюс и минус, вернут либо идентичность значения в случае + i , либо знак, противоположный значению, как в -i .
Умножение и деление
Как сложение и вычитание, умножение и деление будут очень похожи на то, как они действуют в математике. Знак, который мы будем использовать в Python для умножения, - * , а знак, который мы будем использовать для деления, - /.
Вот пример умножения в Python с двумя значениями с плавающей запятой:
к = 100,1
l = 10,1
печать (к * л)
Выход
1011.0099999999999
Когда вы делите в Python 3, ваше частное всегда будет возвращаться как число с плавающей запятой, даже если вы используете два целых числа:
м = 80
п = 5
печать (м / п)
Выход
16.0
Это одно из основных отличий между Python 2 и Python 3. Подход Python 3 дает дробный ответ, поэтому при использовании / для деления 11 на 2 будет возвращено частное 5,5 . В Python 2 частное, возвращаемое для выражения 11/2 , равно 5 .
Оператор / Python 2
выполняет деление этажа , где для частного x возвращаемое число является наибольшим целым числом, меньшим или равным x .Если вы запустите приведенный выше пример print (80/5) с Python 2 вместо Python 3, вы получите 16 в качестве вывода без десятичного разряда.
В Python 3 вы можете использовать // для выполнения разделения этажей. Выражение 100 // 40 вернет значение 2 . Деление этажей полезно, когда вам нужно, чтобы частное было целым.
по модулю
Оператор % представляет собой операцию по модулю, которая возвращает остаток, а не частное после деления.Это полезно, например, для поиска чисел, кратных одному и тому же числу.
Давайте посмотрим на модуль в действии:
o = 85
р = 15
печать (o% p)
Выход
10
Чтобы разбить это, 85, деленное на 15, возвращает частное 5 с остатком 10. Здесь возвращается значение 10 , потому что оператор по модулю возвращает остаток выражения деления.
Если мы используем два числа с плавающей запятой по модулю, для остатка будет возвращено значение с плавающей запятой:
q = 36.0
г = 6,0
печать (o% p)
Выход
0,0
В случае деления 36,0 на 6,0 остатка нет, поэтому возвращается значение 0,0 .
Мощность
Оператор ** в Python используется для возведения числа слева в степень правой степени. То есть в выражении 5 ** 3 5 возводится в 3-ю степень. В математике мы часто видим это выражение в виде 5³, а на самом деле 5 умножается само на себя в 3 раза.В Python мы получили бы тот же результат 125 , выполнив либо 5 ** 3 , либо 5 * 5 * 5 .
Давайте посмотрим на пример с переменными:
с = 52,25
t = 7
печать (дерьмо)
1063173305051.292
Увеличение числа с плавающей запятой 52,25 до степени 7 с помощью оператора ** приводит к возврату большого значения с плавающей запятой.
Приоритет оператора
В Python, как и в математике, мы должны помнить, что операторы будут оцениваться в порядке приоритета, а не слева направо или справа налево.
Если мы посмотрим на следующее выражение:
и = 10 + 10 * 5
Мы можем читать его слева направо, но помните, что сначала будет выполнено умножение, поэтому, если мы вызовем print (u) , мы получим следующее значение:
Выход
60
Это потому, что 10 * 5 оценивается как 50 , а затем мы добавляем 10 , чтобы вернуть 60 в качестве окончательного результата.
Если вместо этого мы хотим добавить значение 10 к 10 , а затем умножить эту сумму на 5 , мы можем использовать круглые скобки так же, как в математике:
ед = (10 + 10) * 5
печать (u)
Выход
100
Один из способов запомнить порядок работы - использовать аббревиатуру PEMDAS :
| Заказать | Письмо | Стенды для |
|---|---|---|
| 1 | п. | P аренцев |
| 2 | E | E xponent |
| 3 | M | M повторение |
| 4 | D | D ivision |
| 5 | А | A ddition |
| 6 | S | S убирание |
Возможно, вы знакомы с другим сокращением порядка операций, например BEDMAS или BODMAS .Какую бы аббревиатуру вы ни выбрали, постарайтесь помнить ее при выполнении математических операций в Python, чтобы получить ожидаемые результаты.
Операторы присваивания
Самый распространенный оператор присваивания - тот, который вы уже использовали: знак равенства = . Оператор присваивания = присваивает значение справа переменной слева. Например, v = 23 присваивает значение целого числа 23 переменной v .
При программировании обычно используются составные операторы присваивания, которые выполняют операцию над значением переменной, а затем присваивают полученное новое значение этой переменной. Эти составные операторы объединяют арифметический оператор с оператором = , поэтому для сложения мы объединим + с = , чтобы получить составной оператор + = . Посмотрим, как это выглядит:
Вт = 5
ш + = 1
печать (ш)
Выход
6
Сначала мы устанавливаем переменную w равной значению 5 , затем мы использовали оператор составного присваивания + = , чтобы добавить правое число к значению левой переменной , а затем присвоить результат Вт .
Операторы составного присваивания часто используются в случае для циклов , которые вы будете использовать, если хотите повторить процесс несколько раз:
для x в диапазоне (0, 7):
х * = 2
печать (х)
Выход
0
2
4
6
8
10
12
С помощью цикла for мы смогли автоматизировать процесс оператора * = , который умножил переменную w на число 2 , а затем присвоил результат переменной w для следующей итерации для цикла.
Python имеет составной оператор присваивания для каждого из арифметических операторов, обсуждаемых в этом руководстве:
y + = 1 # добавить и присвоить значение
y - = 1 # вычесть, затем присвоить значение
y * = 2 # умножить и присвоить значение
y / = 3 # разделить, затем присвоить значение
y // = 5 # разделить этаж, затем присвоить значение
y ** = 2 # увеличить до степени, затем присвоить значение
y% = 3 # вернуть остаток, затем присвоить значение
Операторы составного присваивания могут быть полезны, когда что-то нужно постепенно увеличивать или уменьшать, или когда вам нужно автоматизировать определенные процессы в вашей программе.
Заключение
В этом руководстве рассмотрены многие операторы, которые вы будете использовать с целыми и числовыми типами данных с плавающей запятой. Если вы хотите продолжить чтение о числах в Python, вы можете перейти к встроенным функциям Python 3 для работы с числами.
Чтобы узнать больше о других типах данных, взгляните на Общие сведения о типах данных в Python 3 и узнайте о том, как преобразовывать типы данных, прочитав Как преобразовывать типы данных в Python 3.
Программа Python
для сложения, вычитания, умножения и деления двух чисел
В этом руководстве мы напишем программу Python для сложения, вычитания, умножения и деления двух входных чисел .
Программа для выполнения сложения, вычитания, умножения и деления двух входных чисел в Python
В этой программе пользователя просят ввести два числа и оператор (+ для сложения, - для вычитания, * для умножения и / для деления). Основываясь на вводе, программа вычисляет результат и отображает его как вывод.
Чтобы понять эту программу, вы должны знать, как получить ввод от пользователя, и знать основы оператора if..elif..else.
# Программа опубликована на https: // beginnersbook.ком
# Программа Python для выполнения сложения и вычитания, умножения
# и деление двух чисел
num1 = int (input ("Введите первое число:"))
num2 = int (input ("Введите второе число:"))
print ("Укажите, какую операцию вы хотите выполнить?")
ch = input ("Введите любой из этих символов для конкретной операции +, -, *, /:")
результат = 0
если ch == '+':
результат = число1 + число2
elif ch == '-':
результат = число1 - число2
elif ch == '*':
результат = число1 * число2
elif ch == '/':
результат = число1 / число2
еще:
print («Вводимый символ не распознан!»)
print (num1, ch, num2, ":", результат) Выход 1: Дополнение
Введите первое число: 100 Введите второе число: 5 Введите, какую операцию вы хотите выполнить? Введите любой из этих символов для конкретной операции +, -, *, /: + 100 + 5: 105
Выход 2: Подразделение
Введите первое число: 20 Введите второе число: 5 Введите, какую операцию вы хотите выполнить? Введите любой из этих символов для конкретной операции +, -, *, /: / 20/5: 4.0
Выход 3: вычитание
Введите первое число: 8 Введите второе число: 7 Введите, какую операцию вы хотите выполнить? Введите любой из этих символов для конкретной операции +, -, *, /: - 8–7: 1
Выход 4: умножение
Введите первое число: 6 Введите второе число: 8 Введите, какую операцию вы хотите выполнить? Введите любой из этих символов для конкретной операции +, -, *, /: * 6 * 8: 48
Связанные примеры Python:
1.Программа на Python для сложения двух матриц
2. Программа на Python для сложения двух двоичных чисел
3. Программа на Python для сложения двух чисел
4. Программа на Python для обмена двух чисел
.


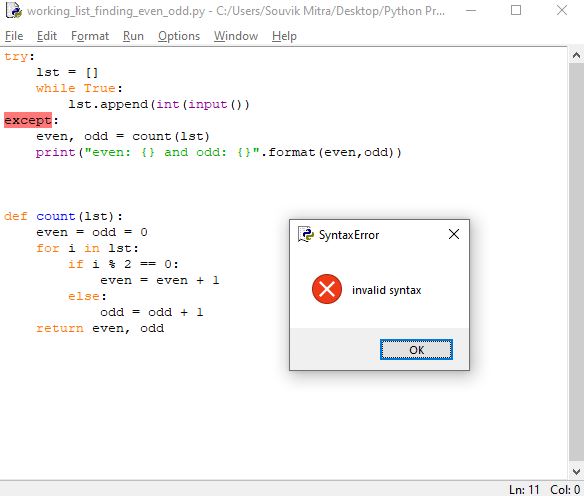 1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.9999999999999999
1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.9999999999999999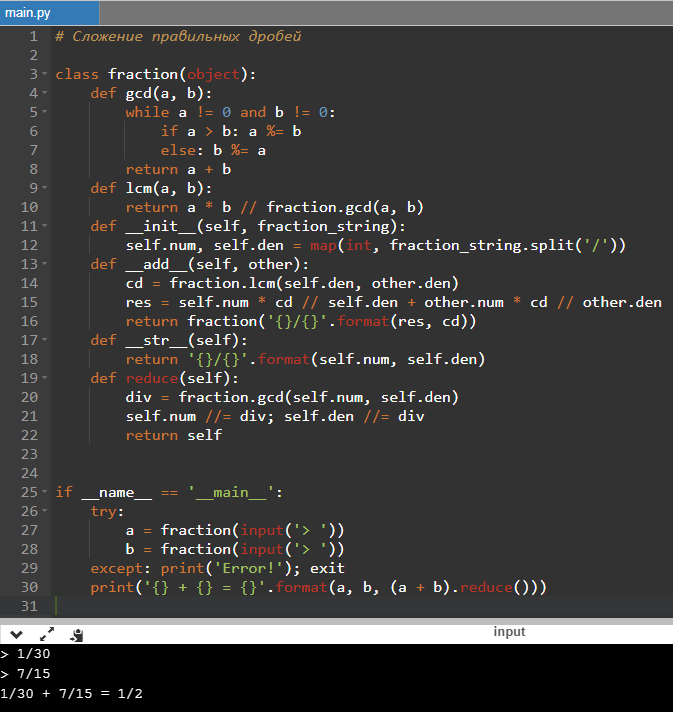 5).hex()
'0x1.5000000000000p+3'
>>> float.fromhex('0x1.5000000000000p+3')
10.5
5).hex()
'0x1.5000000000000p+3'
>>> float.fromhex('0x1.5000000000000p+3')
10.5 conjugate()) # Сопряжённое число
(1-2j)
>>> print(x.imag) # Мнимая часть
2.0
>>> print(x.real) # Действительная часть
1.0
>>> print(x > y) # Комплексные числа нельзя сравнить
Traceback (most recent call last):
File "", line 1, in
TypeError: unorderable types: complex() > complex()
>>> print(x == y) # Но можно проверить на равенство
False
>>> abs(3 + 4j) # Модуль комплексного числа
5.0
>>> pow(3 + 4j, 2) # Возведение в степень
(-7+24j)
conjugate()) # Сопряжённое число
(1-2j)
>>> print(x.imag) # Мнимая часть
2.0
>>> print(x.real) # Действительная часть
1.0
>>> print(x > y) # Комплексные числа нельзя сравнить
Traceback (most recent call last):
File "", line 1, in
TypeError: unorderable types: complex() > complex()
>>> print(x == y) # Но можно проверить на равенство
False
>>> abs(3 + 4j) # Модуль комплексного числа
5.0
>>> pow(3 + 4j, 2) # Возведение в степень
(-7+24j) 0
0 40002000000000004
40002000000000004
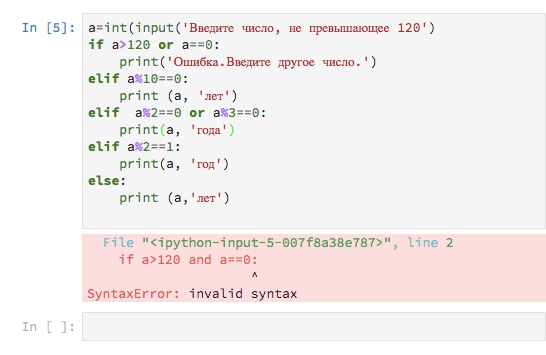 format(z))
format(z))