Двоичная шестнадцатеричная и восьмеричная системы счисления: Двоичная, восьмеричная, шестнадцатеричная системы счисления. Арифметика в указанных системах счисления
Содержание
Информатик БУ — Кратко о системах счисления
Система счисления – это способ записи чисел с помощью символов. Мы все привыкли использовать десять различных знаков для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Такая система счисления называется десятичной. Один знак числа называется цифрой.
Основание системы счисления – это количество знаков, используемых для записи числа в этой системе. Основанием системы счислений, как правило, может являться любое натуральное число (например, шумеры использовали шестидесятеричную систему счисления), но сегодня наиболее распространены (кроме десятичной) двоичная, восьмеричная и шестнадцатеричная. Основание системы счисления указывается подстрочным знаком после числа, например 1012.
Разряд числа – это место цифры в числе. В зависимости от количества разрядов мы называем числа двузначными, трёхзначными, четырёхзначными и т.д.
Двоичная система счисления
Популярность двоичной системы в информатике обусловлена тем, что для записи чисел используется всего две цифры: 0 и 1.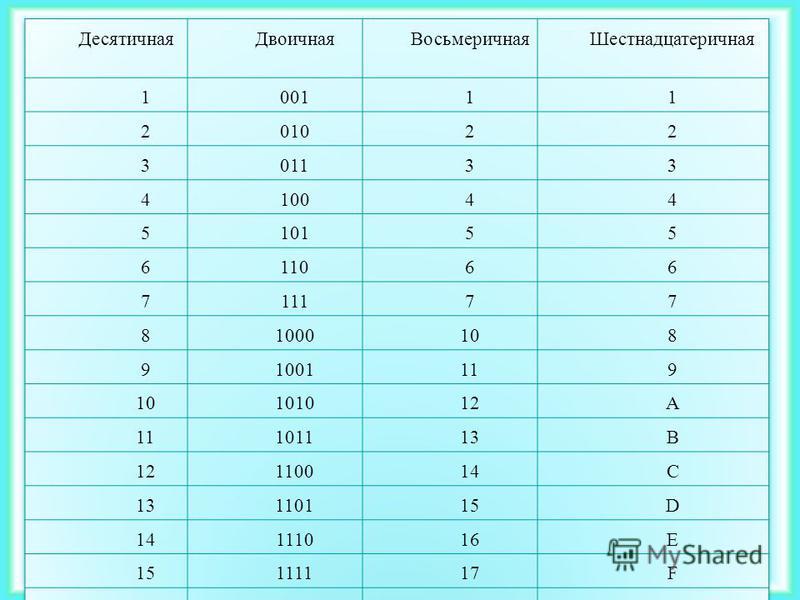 Это соответствует значению одного бита, который тоже может принимать значения 0 и 1. Поэтому во многих случаях один разряд двоичного числа называют битом. А так как в вычислительной технике информация передаётся в битах, то и числа удобнее передавать в виде двоичного (бинарного) кода.
Это соответствует значению одного бита, который тоже может принимать значения 0 и 1. Поэтому во многих случаях один разряд двоичного числа называют битом. А так как в вычислительной технике информация передаётся в битах, то и числа удобнее передавать в виде двоичного (бинарного) кода.
Простой пример. IP-адрес компьютера состоит из четырёх байт, разделенных точками, к примеру:
192.168.0.1
Почему байты записаны в виде чисел? Если перевести байты этого IP-адреса в биты (двоичную систему), мы получим четыре восьмизначных двоичных числа:
11000000. 10101000.00000000.00000001
Двоичные числа состоят из восьми разрядов, а байт равен восьми битам.
Восьмеричная система счисления
Двоичная система счисления удобна для компьютера, но не очень удобна для людей, так как числа, записанные в ней, получаются очень большими по размеру. Представьте, десятичное число 10000000 в двоичной системе выглядит как 100110001001011010000000, не очень удобно, согласитесь?
Поэтому была введена восьмеричная система счисления.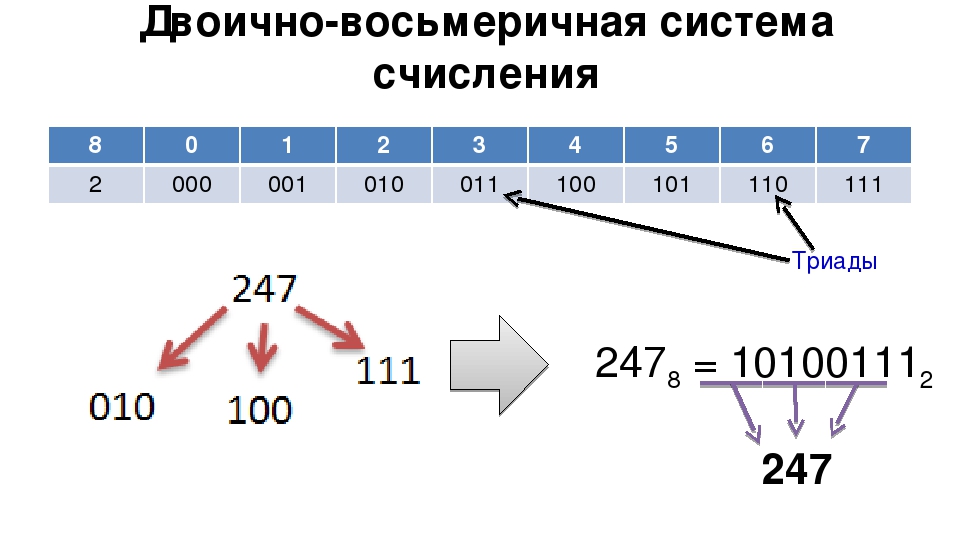 Восьмеричная система отличается от десятичной тем, что двоичные числа очень удобно приводить к основанию 8, а восьмеричные – к основанию 2. С десятичной всё немного сложнее. Для перевода используется таблица триад (в правом нижнем углу сайта есть кнопочка, можете посмотреть, а почитать про правила перевода можно здесь).
Восьмеричная система отличается от десятичной тем, что двоичные числа очень удобно приводить к основанию 8, а восьмеричные – к основанию 2. С десятичной всё немного сложнее. Для перевода используется таблица триад (в правом нижнем углу сайта есть кнопочка, можете посмотреть, а почитать про правила перевода можно здесь).
Шестнадцатеричная система счисления
Помните, что один разряд двоичной системы – это один бит? А два разряда шестнадцатеричной системы – это один байт. В современных компьютерах информация кодируется в байтах, поэтому во многих случаях удобно использовать шестнадцатеричную систему.
В шестнадцатеричной системе шестнадцать разрядов: цифры от 0 до 9, и буквы от A до F (где буквы от A до F – десятичные числа от 10 до 15 соответственно).
Шестнадцатеричную систему используют в низкоуровневом программировании, в компьютерном дизайне широко используются шестнадцатеричные коды цвета, в некоторых кодировках символы кодируются именно с помощью шестнадцатеричной системы… В общем, штука полезная:).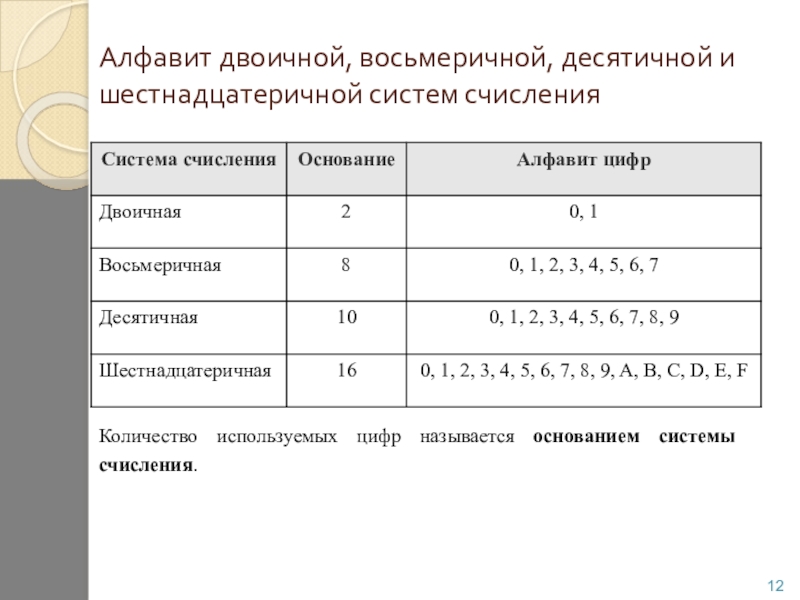
Одно из заданий ЕГЭ предыдущих лет было как раз на знание шестнадцатеричных цветовых кодов.
Пример: нужно определить, какой цвет зашифрован кодом #00FF00 в палитре RGB.
Решение: Данный код является кодом цвета в палитре RGB, то есть первые два разряда – Red, вторые два разряда – Green, третьи два разряда – Blue:
#00FF00
Получается, что красного цвета — 0, синего цвета – 0, а зелёного – FF, то есть 255 в десятичной системе счисления (максимальное двузначное шестнадцатеричное число). То есть это код чистого зелёного цвета.
Подобные коды вы можете встретить, к примеру, в палитре цветов Adobe Photoshop, или при разработке внешнего вида сайта, когда для различных элементов дизайна необходимо указать код цвета.
Восьмеричная система счисления — Программирование на C, C# и Java
Оглавление:
Перевод из десятичной системы счисления в восьмеричную
Перевод из восьмеричной системы счисления в десятичную
Перевод из двоичной системы счисления в восьмеричную
Перевод из восьмеричной системы счисления в двоичную
Перевод из восьмеричной системы счисления в шестнадцатеричную и из шестнадцатеричной системы в восьмеричную
Применение восьмеричной системы счисления
Восьмеричная система – одна из основных систем счислений наряду с двоичной, десятичной и шестнадцатеричной, применяемая в информационных технологиях.
Как мы знаем, компьютеры «воспринимают» лишь двоичную систему счисления, состоящую только из нулей и единиц. Однако человеку довольно непривычно и неудобно работать с такими числами. Например, привычное нам десятичное число 2 143 в двоичной системе будет выглядеть как 100001011111. Переводить числа из двоичной системы в десятеричную также не очень удобно и бывает довольно муторно.
В итоге было решено использовать альтернативные и более простые системы счисления: восьмеричную и шестнадцатеричную. Числа 8 и 16 являются степенями двойки (2 в третьей и 2 в четвёртой степени соответственно), поэтому выполнять преобразования из двоичной системы и наоборот гораздо легче, чем при десятичной системе счисления, которая не может похвастаться своей причастностью к степеням числа 2.
Кроме того, числа в восьмеричной системе как минимум более приятны глазу и гораздо короче, чем их аналоги в двоичной системе. Так, например, в восьмеричной системе то же число 2 143 будет записываться как 4137.
В восьмеричной системе счисления, как уже можно было догадаться, основанием является цифра 8 и, соответственно, она вмещает в себя только восемь цифр: от 0 до 7. Поэтому числа в восьмеричной системе счисления очень похожи на десятичные, в отличие от шестнадцатеричных, где присутствуют буквы латинского алфавита или двоичных, состоящих только из двух цифр. Отличают эти две системы тем, что в восьмеричной отсутствуют цифры 8 и 9, а также, очевидно, нижними индексами: у числа в десятичной системе прибавляют нижний индекс с цифрой 10, а к числам в восьмеричной системе приписывают цифру 8, например:
Теперь давайте научимся переводу чисел в восьмеричную систему счисления и наоборот.
Перевод из десятичной системы счисления в восьмеричную
Давайте попробуем изучить перевод десятичного числа в восьмеричное на примере. После этого примера вы без проблем сможете переводить любые числа в эту систему.
Возьмём десятичное число 15 450 и попробуем перевести его в восьмеричную систему счисления.
Для начала нам необходимо разделить исходное число на основание системы, в которую мы хотим это число перевести. Для восьмеричной системы это число 8. То есть мы делим 15 450 на 8.
Происходит деление в столбик, но, в отличие от стандартного деления, мы не находим неполные частные, а делим сразу всё делимое на 8. Наибольшим числом, при котором 15 450 делится без остатка на 8 будет число 1 931. 1931 * 8 = 15 448. Теперь мы вычитаем из 15 450 полученное число 15 448, у нас получился остаток 2. Выделяем эту двойку, так как это уже кусочек нашего числа в восьмеричной системе.
Продолжаем: теперь делим полученное на предыдущем шаге частное на 8:
Всё точно так же: наибольшим числом, при котором 1 931 делится без остатка на 8 будет число 241. При умножении 241 на 8 получается число 1 928. Ищем разность между 1 931 и 1928 – получается 3. Выделяем её. Далее делим 241 на 8.
Получается число 30, умножив его на 8, получаем 240. Вычитаем из 241 это число, получается 1. Выделяем единицу.
Выделяем единицу.
Продолжаем деление до тех пор, пока частное не станет меньше 8!
Итак, делим 30 на 8, получается 3,75, отбрасываем дробную часть, получается 3. Умножаем 3 на 8, получается 24. 30 – 24 = 6. Выделяем шестёрку. Мы закончили деление так как 3 меньше 8. Обязательно выделяем последнее частное тоже (у нас это цифра 3).
Выделенные красным цифры – это и есть наше число в восьмеричной системе, НО они написаны наоборот. То есть, чтобы правильно прочитать число в восьмеричной системе, необходимо сделать это справа налево.
Таким образом, десятичное число 15 45010 в восьмеричной системе будет выглядеть как 36 1328.
Итого, алгоритм перевода чисел из десятичной системы в восьмеричную следующий:
- Разделить исходное число на 8. Найти максимальное частное и убрать дробную часть от него. Например, исходное число 20 : 8 = 2,5. Значит в частное мы записываем число 2.

- Умножить полученное частное на 8. Записать его под исходным числом.
- Найти остаток между этими числами и выделить его – это кусочек переведённого в восьмеричную систему числа.
- Затем разделить в столбик полученное частное на 8, записать ответ и проделать шаги 2 и 3.
- Производить деление до тех пор, пока делимое не станет меньше 8. Выделить это делимое тоже.
- Выписать все выделенные числа справа налево (т.е. последнее делимое будет на первом месте, затем идёт остаток, найденный на последнем шаге, затем остаток, найденный на предпоследнем шаге и т.д.). Полученное при такой записи число и будет нашим искомым восьмеричным.
Теперь перейдём к переводу восьмеричного числа в десятичную систему счисления.
Перевод из восьмеричной системы счисления в десятичную
Перевести восьмеричное число в десятичное даже проще, чем наоборот. Давайте рассмотрим пример: переведём восьмеричное число 36078 в десятичное.
Для начала мы делаем такую запись: с конца берём каждую цифру нашего исходного числа, каждое из них умножаем на 8, и все в целом складываем. Должно получиться примерно так:
Должно получиться примерно так:
Однако, это ещё не всё! После того, как мы сделали подобную запись, ко всем числам 8, на которые умножаются цифры исходного числа, необходимо добавить степени в порядке возрастания: 0, 1, 2 и т.д. Обязательно необходимо начинать с нулевой степени!
Всё, что остаётся после этого – просто посчитать. В итоге у нас получилось число 1927 в десятичной системе.
Перевод из двоичной системы счисления в восьмеричную
Перевод чисел из двоичной системы счисления в восьмеричную – довольно необычное дело для тех, кто никогда с этим не сталкивался. Однако на деле всё не так пугающе, как может показаться с первого раза.
Давайте попробуем. Допустим, у нас есть двоичное число 1010010001011101100.
Для начала нам необходимо разбить это число на триады – группы из трёх цифр. Почему именно три цифры? Как мы знаем, у систем счислений имеются основания. И у двоичной системы основание – 2. Нам необходимо перевести двоичное число в восьмеричную систему с основанием 8.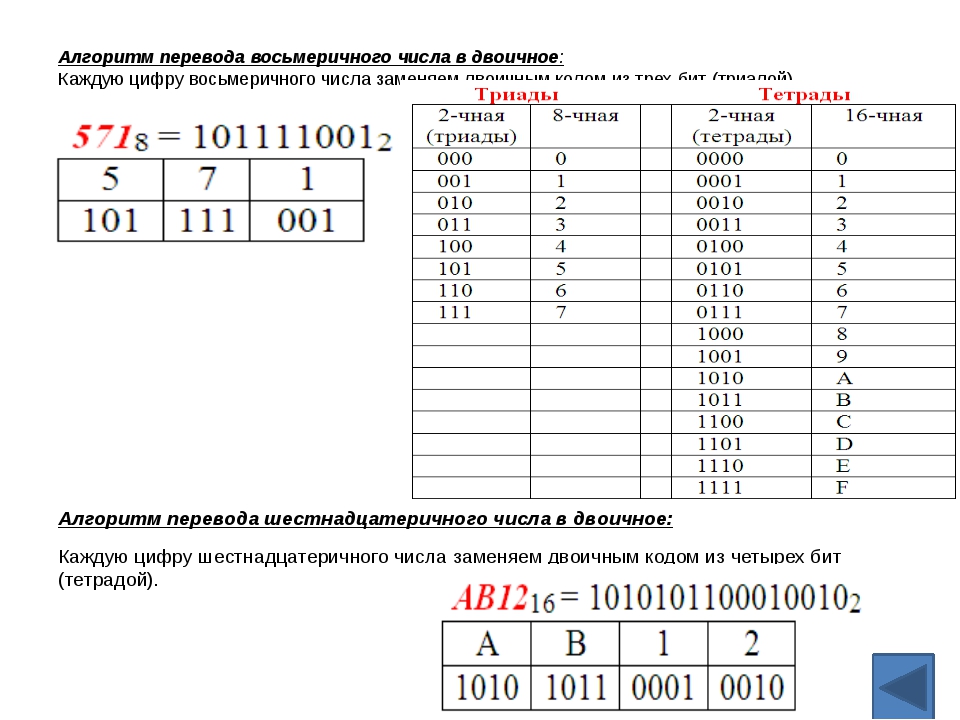 Математически это можно записать так:
Математически это можно записать так:
Найти i, пожалуй, не составит труда: i = 3, то есть, для записи одного восьмеричного числа в двоичной системе необходимо 3 бита или, говоря иначе – 3 двоичные цифры. Поэтому мы и будем разбивать двоичное число на триады. Однако надо запомнить, что делать это надо с младшего бита. Бит – это одна цифра в двоичном числе. Чем дальше бит от начала числа, тем он младше. Самый младший бит – это последняя цифра двоичного числа. Иными словами, мы разбиваем число на триады, начиная с конца.
Внимание: если старшая триада не заполнена, до конца, перед ней необходимо дописать столько нулей, чтобы получилась полноценная триада.
Теперь всё, что нам остаётся – это перевести каждую из этих триад из двоичной системы счисления в восьмеричную. Это можно сделать самостоятельно:
Для этого в каждой отдельной триаде (начиная с первой) нужно каждую цифру (начиная с последней) умножить на 2, возведённую в степени от 0 до 2, и сложить полученные три числа.
Затем, полученные результаты по каждой отдельной триаде надо выписать, начиная с самой первой. Записанное число и будет нашим конечным результатом в восьмеричной системой счисления.
Однако можно сильно облегчить себе задачу, не высчитывая все триады числа, а просто сверяя каждую из них по таблице соответствия двоичных чисел восьмеричным, например, по такой:
Теперь можно просто смотреть на триаду, сверять её с таблицей и записывать число, соответствующее ей в восьмеричной системе.
Перевод из восьмеричной системы счисления в двоичную
Самым удобным способом перевода из восьмеричной системы счисления в двоичную является использование таблицы соответствий. Итак, допустим, мы хотим перевести восьмеричное число 36702 в двоичную систему. Что же нам делать? Мы берём первую цифру нашего исходного числа – 3. Ищем её по таблице соответствия – в двоичной системе это 011. Берём следующую цифру – 6 и ищем её в таблице, находим 110, и так далее. Продолжаем, пока не переведём все восьмеричные цифры в триады. В итоге у нас получится необходимое двоичное число.
В итоге у нас получится необходимое двоичное число.
Внимание: Если в старших битах (то есть в самом начале двоичного числа) имеются нули, необходимо убрать их до первой единицы. Например, как на изображении ниже. В старшем бите у нас получился ноль при переводе восьмеричной тройки, и мы убрали его. Это делается для удобства, потому что зачем хранить и писать незначащие цифры.
Перевод из восьмеричной системы счисления в шестнадцатеричную и из шестнадцатеричной системы в восьмеричную
К сожалению, несмотря на то, что эти системы счисления близки друг к другу, напрямую перевести друг в друга нельзя. Легче всего при переводе этих двух систем друг в друга воспользоваться посредничеством двоичной системы. То есть, перевести восьмеричную систему счисления в двоичную, разделив число на триады и воспользовавшись таблицей соответствий, а затем перевести это число из двоичной системы в шестнадцатеричную с помощью тетрад. И наоборот: перевести число из шестнадцатеричной системы в двоичную, а затем уже из двоичной системы в восьмеричную описанными выше способами.
Применение восьмеричной системы счисления
В прошлом веке выпускались компьютеры, в которых использовались 12-ти, 24-х и 36-битные слова. Это, например, модель ICT 1900 (1964 год), а также PDP-8, выпущенная в 1965 году – это коммерчески довольно успешная модель миникомпьютера в своё время. Кроме того, некоторые мейнфреймы от компании IBM использовали восьмеричную систему. В компьютерах, размер машинного которых кратен тройке, очень удобно использовать систему с основанием восемь, поскольку всегда все биты из слова можно представить в виде целого количества цифр в восьмеричной системе. Например, слово из 24-х бит, можно записать в виде 8-ми восьмеричных чисел.
Если говорить про использование восьмеричной системы в жизни людей, то известно, что в индейских языках Юки (Калифорния) и Паме (Мексика) использовалась данная система. Индейцы считали предметы не по количеству пальцев на руках, а по количеству промежутков между ними.
Восьмеричная система счисления
5 (100%) 12 votes
Поделиться в соц. сетях:
сетях:
Восьмеричная система счисления
☰
При описании двоичной системы счисления было упомянуто, почему современное «железо» понимает только двоичную систему. Однако человеку трудно воспринимать длинные записи нулей и единиц, а переводить числа из двоичной в десятичную систему и обратно трудоемко.
Поэтому в программировании иногда используют другие системы счисления – восьмеричную и шестнадцатеричную. Поскольку 8 и 16 являются степенями двойки,
8 = 23, 16 = 24
преобразование двоичного числа в эти системы, также как обратная операция, выполняются просто.
В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствует число из трех цифр в двоичной системе счисления:
000 – 0 001 – 1 010 – 2 011 – 3 100 – 4 101 – 5 110 – 6 111 – 7
Для преобразования двоичного числа в восьмеричное надо разбить его на тройки цифр и заменить каждую тройку соответствующей ей одной цифрой из восьмеричной системы счисления. Разбивать двоичное число на тройки следует с конца, а вместо недостающих цифр в начале можно записать нули.
Разбивать двоичное число на тройки следует с конца, а вместо недостающих цифр в начале можно записать нули.
1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135
В примере число 1011101 в двоичной системе приводится к числу 135 в восьмеричной системе счисления.
10111012 = 1358
Обратный перевод, когда восьмеричное число переводится в двоичное, выполняется аналогично. Только здесь на место восьмеричных цифр подставляются двоичные числа, состоящие из трех цифр.
135 = 001 011 101
Как перевести восьмеричное число в десятичное? Здесь действует тот же алгоритм, как при преобразовании двоичного числа в десятичное. Вспомним его:
11012 = 1 * 23 + 1 * 22 + 0 * 21 + 1 * 20 = 8 + 4 + 0 + 1 = 1310
Однако в случае восьмеричного числа за основание степени берется десятичное число 8:
1358 = 1 * 82 + 3 * 81 + 5 * 80 = 64 + 24 + 5 = 9310
Преобразование десятичного числа в восьмеричное также похоже на перевод в двоичное, за исключением того, что делить надо на 8:
93 / 8 = 11, остаток 5 11 / 8 = 1, остаток 3 1 / 8 = 0, остаток 1
Собираем остатки с конца и получаем число 135 в восьмеричной системе счисления.
Системы счисления: двоичная, восьмеричная, шестнадцатеричная — 8 КЛАСС ► Информатика в школе и дома
Урок: Системы счисления: двоичная, восьмеричная, шестнадцатеричная
Общие сведения о системах счисления
С древних времен в практической деятельности человека часто возникала потребность счета и измерения. Результаты счета предметов выражались вначале весьма примитивно: зарубки на палочках, узелки на веревках и др. С развитием письменности человек начал отображать с помощью знаков (записывать) информацию о количестве предметов на подручных материалах: глиняных табличках, папирусе, бересте и др. Таким образом, для обозначения чисел стали использовать знаки.
Способ записи чисел с помощью письменных знаков называют системой счисления. Знаки, с помощью которых записываются числа, называют цифрами, а их совокупность — алфавитом системы счисления.
Одной из наиболее древних являлась египетская иероглифическая система счисления. В ней числа представлялись в виде отдельных знаков, например:
В ней числа представлялись в виде отдельных знаков, например:
Так, число означало:
100+10+10+1+1+1=123.
Существовали системы счисления, в которых для записи чисел использовались буквы алфавита, например старославянская система счисления.
Десятичная система счисления зародилась в Индии приблизительно в 5 в., затем она появилась в арабских рукописях. Из арабских рукописей эта система пришла в Европу в 9-12 вв. Поэтому современную десятичную систему счисления называют арабской.
В любой системе счисления цифры служат для обозначения чисел, называемых узловыми; остальные числа (алгоритмические) получаются в результате каких-либо операций из узловых чисел.
Пример:
У вавилонян узловыми являлись числа 1, 10, 60; в римской системе счисления узловые числа — это 1, 5, 10, 50, 100, 500 и 1000, обозначаемые соответственно I, V, X, L, C, D, M.
Системы счисления различаются выбором узловых чисел и способами образования алгоритмических чисел.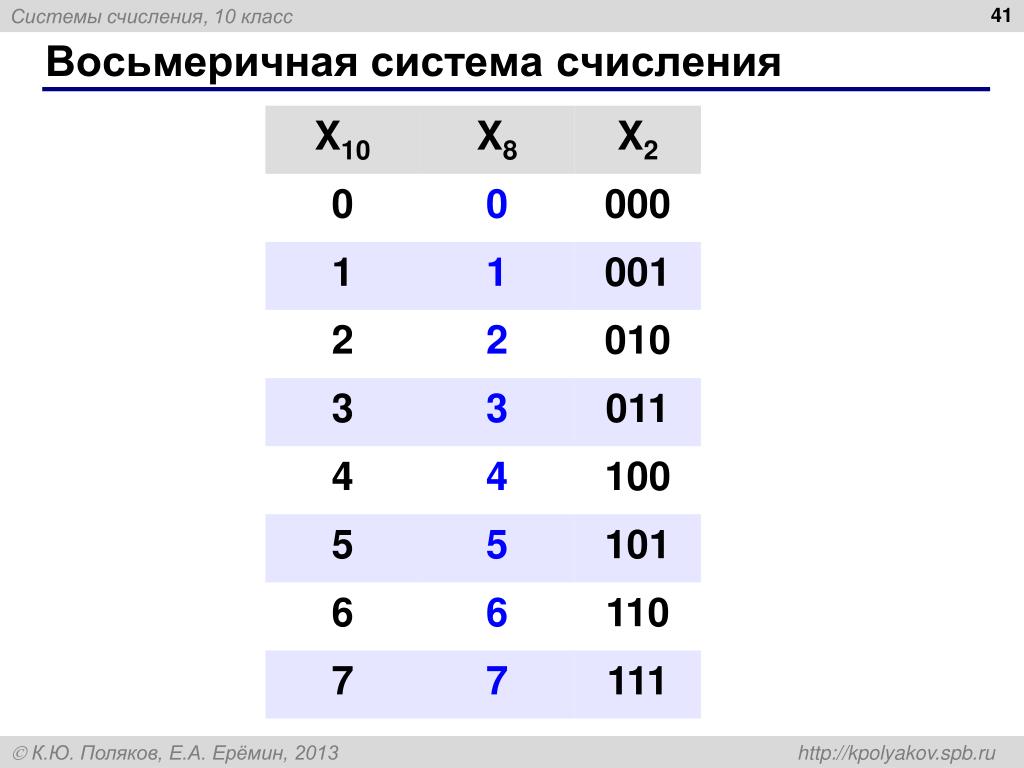 Можно выделить следующие виды систем счисления:
Можно выделить следующие виды систем счисления:
- унарная система;
- непозиционные системы;
- позиционные системы.
Простейшая и самая древняя система — так называемая унарная система счисления.
В ней для записи любых чисел используется всего один символ — палочка, узелок, зарубка, камушек. Длина записи числа при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков. Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит первоклассников в мир счёта.
Унарную систему ещё называют системой бирок.
Непозиционными называются такие системы счисления, в которых каждый знак (цифра) в записи любого числа имеет одно и то же значение и не зависит от своего расположения в числе.
В большинстве непозиционных систем счисления числа образуются путём сложения узловых чисел.
В непозиционной римской системе счисления для обозначения чисел используются следующие знаки:
Например, число записанное в римской системе счисления, в десятичной системе счисления означает: 10+10+5+1+1+1=28.
Древнеегипетская и старославянская система также являются непозиционными.
Позиционными называют такие системы счисления, в которых значение каждого знака (цифры) в записи любого числа зависит от расположения (позиции) этого знака в числе. Количество цифр, используемых для записи чисел в позиционной системе счисления, называется ее основанием.
Мы используем позиционную десятичную систему счисления. Основанием этой системы является число 10.
Для записи любого числа в десятичной системе счисления используют десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Комбинируя эти цифры, можно записывать любые числа.
Например, цифры числа 737 в десятичной системе счисления являются коэффициентами его записи в виде суммы степеней числа 10:
737=7⋅102+3⋅101+7⋅100=7⋅100+3⋅10+7⋅1
Из этого примера видно, что цифра 7 в зависимости от своей позиции в этом числе означает и 7 сотен, и 7 единиц, а цифра 3 означает три десятка.
Пример:
Рассмотрим десятичное число 13456,7. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развернутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:
Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развернутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:
1⋅104+3⋅103+4⋅102+5⋅101+6⋅100+7⋅10−1.
Системы счисления: двоичная, восьмеричная, шестнадцатеричная
Для кодирования информации в компьютере вместо привычной десятичной системы счисления используется двоичная система счисления.
Двоичной системой счисления люди начали пользоваться очень давно. Древние племена Австралии и островов Полинезии использовали эту систему в быту. Так, полинезийцы передавали необходимую информацию, выполняя два вида ударов по барабану: звонкий и глухой. Это было примитивное представление двоичной системы счисления.
Двоичной системой счисления называется позиционная система счисления с основанием 2.
Для записи чисел в ней использовали только две цифры: 0 и 1.
Для обозначения системы счисления, в которой представляется число, используют нижний индекс, указывающий основание системы. Например, 110112 — число в двоичной системе счисления.
Например, 110112 — число в двоичной системе счисления.
Цифры в двоичном числе являются коэффициентами его представления в виде суммы степеней с основанием 2, например:
1012=1⋅22+0⋅21+1⋅20.
В десятичной системе счисления это число будет выглядеть так:
1012=4+0+1=5.
Для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример:
Переведём десятичное число 13 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:
Получили 1310=11012.
Пример:
Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:
22410=111000002.
Восьмеричной системой счисления называется позиционная система счисления с основанием 8.
Для записи чисел в восьмеричной системе счисления используются цифры: 0, 1, 2, 3, 4, 5, 6, 7.
Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в восьмеричной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример:
Переведём восьмеричное число 154368 в десятичную систему счисления.
154368=1⋅84+5⋅83+4⋅82+3⋅81+6⋅80=694210
Пример:
Переведём десятичное число 94 в восьмеричную систему счисления.
9410=1368
Шестнадцатеричной системой счисления называется позиционная система счисления с основанием 16.
Для записи чисел в шестнадцатеричной системе счисления используются цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и латинские буквы A, B, C, D, E, F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510.
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Для перевода целого десятичного числа в шестнадцатеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 16 до тех пор, пока не получим частное, равное нулю. Исходное число в системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример:
Переведём шестнадцатеричное число 2A7 в десятичное. В соответствии с вышеуказанными правилом представим его в виде суммы степеней с основанием 16:
2A716=2⋅162+10⋅161+7⋅160=512+160+7=679.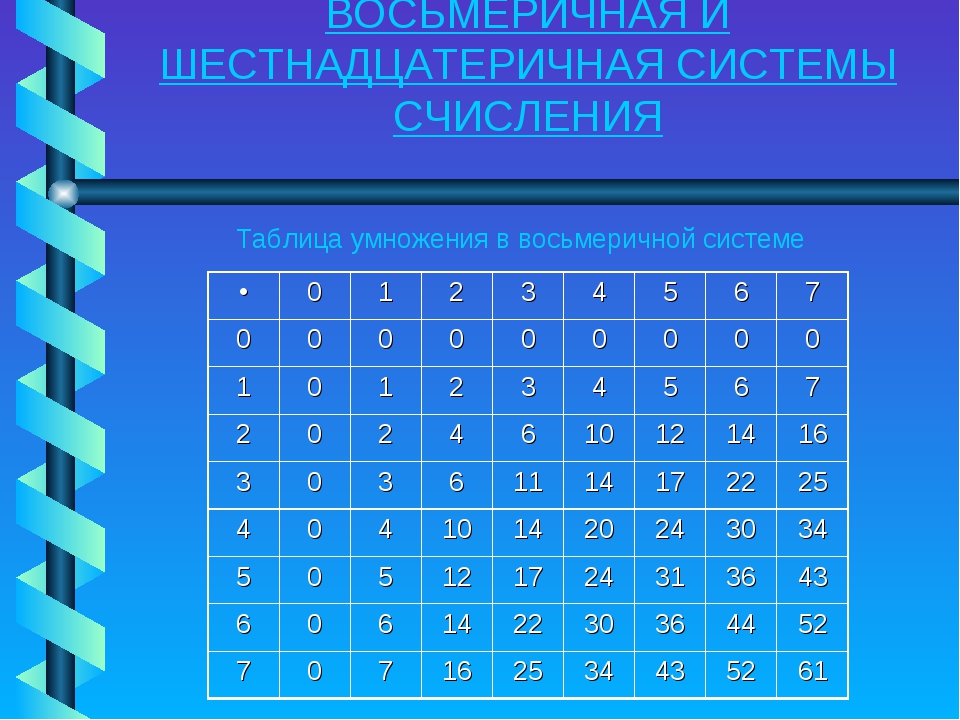
Пример:
Переведём десятичное число 158 в шестнадцатеричную систему счисления.
15810=9E16.
Для перевода числа из любой позиционной системы счисления в десятичную необходима использовать развернутую формулу числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами.
Для перевода целых чисел десятичной системы счисления в число любой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы счисление, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.
Рекомендованный список литературы
Босова Л.Л. Информатика — Учебник для 8 класса. – М.: БИНОМ. Лаборатория знаний
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 0 1 2 3 4 5 6 7 8 9 A B C D E F | 000 001 002 003 004 005 006 007 010 011 012 013 014 015 016 017 | 00000000 00000001 00000010 00000011 00000100 00000101 00000110 00000111 00001000 00001001 00001010 00001011 00001100 00001101 00001110 00001111 |
| 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F | 020 021 022 023 024 025 026 027 030 031 032 033 034 035 036 037 | 00010000 00010001 00010010 00010011 00010100 00010101 00010110 00010111 00011000 00011001 00011010 00011011 00011100 00011101 00011110 00011111 |
| Десятичное Dec | Шестнадцатеричное Hex | Восьмеричное Oct | Двоичное Bin |
| 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 | 20 21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F | 040 041 042 043 044 045 046 047 050 051 052 053 054 055 056 057 | 00100000 00100001 00100010 00100011 00100100 00100101 00100110 00100111 00101000 00101001 00101010 00101011 00101100 00101101 00101110 00101111 |
| 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 | 30 31 32 33 34 35 36 37 38 39 3A 3B 3C 3D 3E 3F | 060 061 062 063 064 065 066 067 070 071 072 073 074 075 076 077 | 00110000 00110001 00110010 00110011 00110100 00110101 00110110 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111 |
| Десятичное Dec | Шестнадцатеричное Hex | Восьмеричное Oct | Двоичное Bin |
| 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 | 40 41 42 43 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F | 100 101 102 103 104 105 106 107 110 111 112 113 114 115 116 117 | 01000000 01000001 01000010 01000011 01000100 01000101 01000110 01000111 01001000 01001001 01001010 01001011 01001100 01001101 01001110 01001111 |
| 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 | 50 51 52 53 54 55 56 57 58 59 5A 5B 5C 5D 5E 5F | 120 121 122 123 124 125 126 127 130 131 132 133 134 135 136 137 | 01010000 01010001 01010010 01010011 01010100 01010101 01010110 01010111 01011000 01011001 01011010 01011011 01011100 01011101 01011110 01011111 |
| 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 | 60 61 62 63 64 65 66 67 68 69 6A 6B 6C 6D 6E 6F | 140 141 142 143 144 145 146 147 150 151 152 153 154 155 156 157 | 01100000 01100001 01100010 01100011 01100100 01100101 01100110 01100111 01101000 01101001 01101010 01101011 01101100 01101101 01101110 01101111 |
| Десятичное Dec | Шестнадцатеричное Hex | Восьмеричное Oct | Двоичное Bin |
| 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 | 70 71 72 73 74 75 76 77 78 79 7A 7B 7C 7D 7E 7F | 160 161 162 163 164 165 166 167 170 171 172 173 174 175 176 177 | 01110000 01110001 01110010 01110011 01110100 01110101 01110110 01110111 01111000 01111001 01111010 01111011 01111100 01111101 01111110 01111111 |
| 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 | 80 81 82 83 84 85 86 87 88 89 8A 8B 8C 8D 8E 8F | 200 201 202 203 204 205 206 207 210 211 212 213 214 215 216 217 | 10000000 10000001 10000010 10000011 10000100 10000101 10000110 10000111 10001000 10001001 10001010 10001011 10001100 10001101 10001110 10001111 |
| 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 | 90 91 92 93 94 95 96 97 98 99 9A 9B 9C 9D 9E 9F | 220 221 222 223 224 225 226 227 230 231 232 233 234 235 236 237 | 10010000 10010001 10010010 10010011 10010100 10010101 10010110 10010111 10011000 10011001 10011010 10011011 10011100 10011101 10011110 10011111 |
| Десятичное Dec | Шестнадцатеричное Hex | Восьмеричное Oct | Двоичное Bin |
| 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 | A0 A1 A2 A3 A4 A5 A6 A7 A8 A9 AA AB AC AD AE AF | 240 241 242 243 244 245 246 247 250 251 252 253 254 255 256 257 | 10100000 10100001 10100010 10100011 10100100 10100101 10100110 10100111 10101000 10101001 10101010 10101011 10101100 10101101 10101110 10101111 |
| 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 | B0 B1 B2 B3 B4 B5 B6 B7 B8 B9 BA BB BC BD BE BF | 260 261 262 263 264 265 266 267 270 271 272 273 274 275 276 277 | 10110000 10110001 10110010 10110011 10110100 10110101 10110110 10110111 10111000 10111001 10111010 10111011 10111100 10111101 10111110 10111111 |
| Десятичное Dec | Шестнадцатеричное Hex | Восьмеричное Oct | Двоичное Bin |
| 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 | C0 C1 C2 C3 C4 C5 C6 C7 C8 C9 CA CB CC CD CE CF | 300 301 302 303 304 305 306 307 310 311 312 313 314 315 316 317 | 11000000 11000001 11000010 11000011 11000100 11000101 11000110 11000111 11001000 11001001 11001010 11001011 11001100 11001101 11001110 11001111 |
| 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 | D0 D1 D2 D3 D4 D5 D6 D7 D8 D9 DA DB DC DD DE DF | 320 321 322 323 324 325 326 327 330 331 332 333 334 335 336 337 | 11010000 11010001 11010010 11010011 11010100 11010101 11010110 11010111 11011000 11011001 11011010 11011011 11011100 11011101 11011110 11011111 |
| 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 | E0 E1 E2 E3 E4 E5 E6 E7 E8 E9 EA EB EC ED EE EF | 340 341 342 343 344 345 346 347 350 351 352 353 354 355 356 357 | 11100000 11100001 11100010 11100011 11100100 11100101 11100110 11100111 11101000 11101001 11101010 11101011 11101100 11101101 11101110 11101111 |
| Десятичное Dec | Шестнадцатеричное Hex | Восьмеричное Oct | Двоичное Bin |
| 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 | F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 FA FB FC FD FE FF | 360 361 362 363 364 365 366 367 370 371 372 373 374 375 376 377 | 11110000 11110001 11110010 11110011 11110100 11110101 11110110 11110111 11111000 11111001 11111010 11111011 11111100 11111101 11111110 11111111 |
Конспект урока: » Системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная.
 Перевод целых чисел из одной системы счисления в другую «.
Перевод целых чисел из одной системы счисления в другую «.
Урок 2
Учитель: Асылбекова Л. С. Класс: 8 Дата: ______________
Тема урока: » Системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная. Перевод целых чисел из одной системы счисления в другую «.
Цель урока: дать первичное представление о структуре компьютерной памяти, системах счисления.
Задачи:
актуализация изученных ранее в курсе математики подходы к представлению числовой информации;
развитие эмоционально-эстетической отзывчивости учащихся средствами комплексного воздействия информационных технологий;
воспитание интерес к историческим сведениям.
Ход урока:
Изучение нового материала
Общие сведения о системах счисления
Под системой счисления принято понимать совокупность приемов записи чисел. Условные знаки, которые при этом применяются, называют цифрами. В некоторых системах счисления кроме цифр могут использоваться специальные символы. Таким образом, в системах счислениях числа записываются как последовательность цифр или специальных символов. Системы счисления подразделяются на позиционные и непозиционные.
В непозиционной системе счисления значение цифры не зависит от ее положения в записи числа. К непозиционной системе счисления относится, так называемая, Римская система счисления. Например, возьмем число ХХХ из Римской системы счисления. В данном числе цифра Х в любом месте означает число десять.
В позиционных системах счисления значение каждой цифры зависит от ее положения (позиции) в ряду цифр, изображающих это число. Например, в числе 999 (десятичная система счисления) первая справа цифра 9 означает количество единиц, содержащихся в числе, вторая – количество десятков, третья – количество сотен. Принимая за основание системы различные числа можно получить соответствующие системы счисления. Число Р единиц одного разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления, а сама система называется Р-ичной. Поэтому для записи произвольного числа в какой-либо позиционной системе счисления достаточно иметь Р различных цифр. Таким образом, любая позиционная система с любым целым основанием Р (при Р1) использует Р различных цифр а, которые обозначают последовательный ряд чисел от 0 и кончая числом Р-1. Эти цифры называются базисными.
Число записывается в виде последовательности Р-ичных цифр, которая разделена точкой на целую и дробную части. Если каждый из символов означает некоторую Р-ичную цифру, то запись числа имеет вид . Каждой цифре из этой последовательности принято определенное значение. Цифра, стоящая в некотором разряде, имеет значение в Р раз больше того, которое она имела бы в разряде с номером, меньшим на 1. И наоборот, в Р раз меньшее того, которое она имела бы в разряде с номером, большим на 1.
2. Позиционные системы счисления
Как было сказано, количество различных цифр, применяемых в позиционной системе счисления, называют ее основанием. Принимая за основание системы различные числа можно получить соответствующие системы счисления. К позиционным системам счисления, получившим наибольшее распространение, относятся десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления. Для того, чтобы отличать в какой системе представлено то или иное число, в дальнейшем будем записывать число с указанием используемой системы счисления. Например, — число 375 в десятичной системе счисления, а число — число 375 в восьмеричной системе счисления.
2.1. Десятичная система счисления
Это наиболее широко распространенная система счисления, которая использует 10 различных базисных цифр для представления любой величины. При записи чисел в десятичной системе счисления используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Несмотря на простоту и привычность десятичной системы счисления использование ее при передачи информации в вычислительных машинах представляется неудобной и технически не экономичной. Поэтому при организации вычислительных процессов в ЭВМ используются системы счисления с другими основаниями.
2.2. Двоичная система счисления
Большинство элементов, из которых строится ЭВМ, по своей физической природе могут находиться лишь в одном из двух состояний. Такие элементы называются двухпозиционными. Одно из устойчивых состояний элемента принимается за изображение цифры 0, а другое за изображение цифры 1. С помощью двухпозиционных элементов легко изображаются разряды двоичного числа. Поэтому двоичная система счисления имеет преимущества, и она оказывается очень удобной для применения в ЭВМ. Двоичная система счисления имеет только две цифры: 0 и 1. Это минимальное количество цифр, которое может быть принято в системе счисления.
Как и в десятичной системе счисления, в двоичной системе для отделения дробной части от целой используется точка, а перед отрицательным числом ставится минус (-):
2.3 Восьмеричная система счисления
В цифровых схемах и в электронных системах получила распространение восьмеричная система счисления. Данная система удобна тем, что восьмеричная запись какого-либо числа в три раза короче его двоичной записи. В данной системе счисления коэффициенты а принимают восемь различных значений — 0, 1, 2, 3, 4, 5, 6, 7.
Поскольку , то каждый восьмеричный символ может быть представлен трехбитовым числом. Этих чисел восемь, как и символов в восьмеричной системе счисления. Как и в рассмотренных системах счисления, в восьмеричной системе используются дробные и отрицательные числа:
2.4. Шестнадцатеричная система счисления
Для систем счисления с основанием больше “10”, арабских цифр для представления чисел не хватит. Поэтому в этих случаях дополнительно вводят специальные символы. К таким системам счисления относится шестнадцатеричная система счисления.
В шестнадцатеричной системе счисления используются 16 базисных символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F. Выбор шестнадцатеричной системы счисления обуславливается тем, что , т.е. эту систему можно использовать как средство сокращенной записи четырехразрядного двоичного числа.
Следует помнить, что шестнадцатеричные и восьмеричные числа – это только способ представления двоичных чисел.
Для представления дробных и отрицательных шестнадцатеричных чисел используется, соответственно, точка и знак минуса (-):
3. Перевод чисел в позиционных системах счисления
3.1. Перевод из десятичной системы счисления
Для перевода целого десятичного числа в другую систему счисления, необходимо разделить исходное число на основание системы счисления в которое оно переводится. При этом надо определять остатки деления. Остаток первого деления является значением младшего разряда. Затем полученное частное делится на выбранное основание. Процедуру деления продолжают до тех пор пока не станет меньше делителя, т.е. основания системы счисления, в которую осуществляется перевод. Значение последнего частного будет наибольшим разрядом, т.е. запись нового числа производится в обратном порядке: от частного к первому остатку, используя все промежуточные остатки.
При переводе в шестнадцатеричную систему счисления остатки, значения которых больше 9, необходимо заменить соответствующим буквенным эквивалентом: 10-А, 11-В, 12-С, 13-D, 14-E, 15-F.
Пример перевода целого десятичного числа 95:
а) в двоичную систему счисления
95 2
94 47 2
1 46 23 2
1 22 11 2
1 10 5 2
1 4 2 2
1 2 1
0 Место для формулы.
б) в восьмеричную систему счисления
95 8
88 11 8
7 8 1
3
в) в шестнадцатеричную систему счисления
95 16
80 5
15
При переводе правильных десятичных дробей, необходимо умножить значение этой дроби на основание системы счисления, в которую осуществляется перевод. Значение целой части результата первого умножения присваивается старшему разряду дробной части. Затем целая часть не рассматривается и производится следующее умножение дробной части. Процедуру умножения повторяют до тех пор, пока результат умножения не будет равен целому числу и этот результат будет младшим разрядом, либо не будет достигнута требуемая точность.
Примеры перевода правильной десятичной дроби 0.36:
а) в двоичную
*0.36
2
*0.72
2
*1.44
2
*0.88
2
1.76
0.3610 = 0.01012
б) в восьмеричную
*0.36
8
*2.88
8
*7.04
8
*0.32
8
2.56
0.3610 = 0.27028
в) в шестнадцатеричную
*0.36
16
*5.76
16
*12.16
16
*2.56
16
8.96
0.3610 = 0.5C281
Для перевода неправильной десятичной дроби, необходимо перевести отдельно дробную и целую часть, а полученные результаты сложить.
Например, перевести в двоичную систему счисления неправильную десятичную дробь 14.375.
1410 = 11102 0.37510 = 0.0112 14.37510 = 1110.0112
Перевод в десятичную систему счисления
Для перевода из любой позиционной системы счисления в десятичную систему счисления необходимо записать это число в виде суммы:
где Р – основание системы из которой осуществляется перевод; a – число, соответствующее базисной цифре Р-ичной системы счисления; n – число цифр в целой части; m – число цифр в дробной части.
Например, перевести число 110.101 из двоичной системы счисления в десятичную:
110.1012 = 1*22 + 1*21 + 0*20 + 1*2-1 + 0*2-2 + 1*2-3 = 6.62510
Для удобства расчета в табл. 1 приведены значения степеней позиционных систем счисления.
Таблица 1.
Значения степеней позиционных систем счисления
Степень Основание | 4 | 3 | 2 | 1 | -1 | -2 | -3 |
2 | 16 | 8 | 4 | 2 | 0.5 | 0.25 | 0.125 |
8 | 4096 | 512 | 64 | 8 | 0.125 | 0.0156 | 0.002 |
16 | 65536 | 4096 | 256 | 16 | 0.0625 | 0.004 | 0.0002 |
Перевод из двоичной системы счисления в восьмеричную и шестнадцатеричную
Основания восьмеричной и шестнадцатеричной систем счисления (q) являются степенью основания двоичной системы (p) : q = pk , где k – целое число, равное 3 для восьмеричной системы счисления и 4 для шестнадцатеричной. Поэтому перевод из двоичной системы осуществляется разбиением двоичного числа на группы по три цифры в каждой для восьмеричной и по четыре для шестнадцатеричной. Отчет ведется от точки разделяющей целую часть от дробной в обе стороны. Затем каждая группа заменяется соответствующей цифрой из соответствующих систем счисления (см. табл. 2 и 3). Недостающие биты двоичного числа дополняются нулями: впереди – для целой части и в конце – для дробной части. Например, необходимо перевести двоичное число 1010001110.00111 в восьмеричное и шестнадцатеричное число:
а) в восьмеричное
1010001100.001112 = 001 010 001 100.001 1102 = 1214.168
б) в шестнадцатеричное
1010001100.001112 = 0010 1000 1100.0011 10002 = 28С.3816
Таблица 2. Таблица 3.
Двоичные – восьмеричные Двоичные – шестнадцатеричные
0000 – 0 0001 – 1 0010 – 2 0011 – 3 0100 – 4 0101 – 5 0110 – 6 0111 – 7 1000 – 8 1001 – 9 1010 – А 1011 – В 1100 – С 1101 – D 1110 – E 1111 — F |
Перевод в двоичную систему счисления
из восьмеричной и шестнадцатеричной
Для перевода в двоичную систему из восьмеричной или шестнадцатеричной систем счисления необходимо каждое число заменить двоичным эквивалентом (см. табл.2 и 3). Например: 34.58 = 011 100.1012 ; A3.E16 = 1010 0011.11102.
Перевод из восьмеричной системы в шестнадцатеричную
Для перевода из восьмеричной системы счисления в шестнадцатеричную систему счисления необходимо представить это число в виде двоичного числа. Затем объединить в группы по 4 бита и заменить соответствующим числом из шестнадцатеричной системы счисления (см. табл.2 и 3). Например: 3458 = 011 100 1012 = 0111001012 = Е516
Перевод из шестнадцатеричной системы в восьмеричную
Для перевода шестнадцатеричной системы счисления в восьмеричную необходимо представить это число в виде двоичного числа. Затем объединить в группы по 3 бита и заменить соответствующим числом из восьмеричной системы счисления (см. табл.2 и 3). Например: В516 = 1011 01012 = 010 110 1012 = 2658
Вопросы учащихся.
Подведение итогов. Выставление оценок.
Домашнее задание п.2-3 стр 7-13 ПЗ в учебнике
5
Как перевести число из двоичной системы в восьмеричную и шестнадцатеричную
- Главная
- Справочник
- Информатика
- Основы
- Как перевести число из двоичной системы в восьмеричную и шестнадцатеричную
Перевод чисел из двоичной системы счисления в восьмеричную, шестнадцатеричную или четвертичную и наоборот часто требуется для решения задач по теме Системы счисления. Чтобы перевести число из одной системы в другую, нужно использовать таблицу перевода чисел.
Таблица перевода чисел
| Десятичная СС | Двоичная СС | Четвертичная СС | Восьмеричная СС | Шестнадцатеричная СС |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 | 2 |
| 3 | 11 | 3 | 3 | 3 |
| 4 | 100 | 10 | 4 | 4 |
| 5 | 101 | 11 | 5 | 5 |
| 6 | 110 | 12 | 6 | 6 |
| 7 | 111 | 13 | 7 | 7 |
| 8 | 1000 | 20 | 10 | 8 |
| 9 | 1001 | 21 | 11 | 9 |
| 10 | 1010 | 22 | 12 | A |
| 11 | 1011 | 23 | 13 | B |
| 12 | 1100 | 30 | 14 | C |
| 13 | 1101 | 31 | 15 | D |
| 14 | 1110 | 32 | 16 | E |
| 15 | 1111 | 33 | 17 | F |
| 16 | 10000 | 100 | 20 | 10 |
Как перевести число из двоичной системы счисления
Чтобы перевести число из двоичной системы счисления в четвертичную, восьмеричную или шестнадцатеричную систему, нужно воспользоваться алгоритмом перевода:
- Разбить двоичное число справа налево на группы по 2 (для четвертичной СС), 3 (для восьмеричной СС) или 4 (для шестнадцатеричной СС) цифры. Если слева не будет хватать цифр для полной группы, нужно дописать необходимое количество незначащих нулей.
- Заменить каждую группу цифр на ее аналог в соответствующей системе счисления.
Как перевести число в двоичную систему счисления
Чтобы перевести число из четвертичной, восьмеричной или шестнадцатеричной системы счисления в двоичную, нужно воспользоваться алгоритмом перевода:
- Заменить каждую цифру на двоичный аналог, состоящий из 2 (для четвертичной), 3 (для восьмеричной) или 4 (для шестнадцатеричной) цифр. Если нужно, число дополняется нулями слева.
- Вычеркнуть из числа незначащие нули.
Онлайн калькулятор перевода чисел из одной системы счисления в любую другую
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Системы счисления — десятичные, двоичные, восьмеричные и шестнадцатеричные | Рукшани Атхапату | Coder’s Corner
Изображение предоставлено: Pexels
Давайте рассмотрим несколько различных систем счисления, которые используются сегодня, и посмотрим, как с помощью трех простых правил мы можем построить любую систему счисления, какую захотим.
В математике «основание» или «основание» — это количество различных цифр или комбинации цифр и букв, которые система счета использует для представления чисел. ~ Wiki ~
Например,
- Base 10 ( Decimal) — Представляет любое число, используя 10 цифр [0–9]
- Base 2 ( Binary ) — Представляет любое число, используя 2 цифры [0 –1]
- Base 8 ( Octal ) — представляет любое число, используя 8 цифр [0–7]
- Base 16 (Hexadecimal) — Представляет любое число, используя 10 цифр и 6 символов [0–9, A, B, C, D, E, F]
В любой из упомянутых выше систем счисления ноль очень важен как значение места.Возьмем число 1005. Как нам записать это число, чтобы знать, что в нем нет десятков и сотен? Мы не можем записать его как 15, потому что это другое число, а как записать миллион (1000000) или миллиард (1000000000) без нулей? Вы понимаете это значение?
Сначала мы увидим, как построена десятичная система счисления, а затем мы будем использовать те же правила и для других систем счисления.
Мы все умеем писать числа до 9, не так ли? Что тогда? Что ж, это действительно просто.Когда вы израсходуете все свои символы, вы сделаете
- , вы добавите еще одну цифру слева и сделаете правую цифру 0.
- Затем снова поднимитесь до, пока не закончите все символы с правой стороны. и когда вы нажмете последний символ, увеличьте цифру слева на 1.
- Когда вы израсходуете все символы как на правой, так и на левой цифре, сделайте оба из них 0 и добавьте еще 1 слева, и это продолжится. и тому подобное.
Если вы используете 3 приведенных выше правила в десятичной системе,
- Запишите числа 0–9.
- Как только вы дойдете до 9, сделайте крайнюю правую цифру 0 и прибавьте 1 к левой, что означает 10.
- Затем на правой цифре мы продвинемся до 9, а когда мы достигнем 19, мы используем 0 на правой цифре и добавим 1 к слева, поэтому мы получаем 20.
- Точно так же, когда мы достигаем 99, мы используем 0 в местах обеих этих цифр и добавляем 1 слева, что дает нам 100.
Итак, вы видите, когда у нас есть десять разных символов, когда мы добавляем цифры в левую часть числа, каждая позиция будет стоить в 10 раз больше, чем предыдущая.
Возьмем ту же десятичную систему счисления. На самом деле есть только два правила.
- У вас есть символ для представления количества [0–9]
- Затем значение цифры в зависимости от ее положения — давайте это немного проясним.
Возьмем однозначное число «8». Это просто означает 8, другими словами, это именно то, что, как написано, представляет. А как насчет 24? В случае двух цифр правая цифра говорит то, что она означает, а левая цифра означает в десять раз больше, чем она говорит.То есть 4 равно 4, 2 равно 20. Всего получается 24.
Если мы возьмем трехзначное число, крайняя правая цифра означает то, что оно говорит, средняя цифра в десять раз больше того, что она говорит, а крайняя левая цифра в 100 раз больше того, что она говорит. Просто, если мы возьмем число 546, это означает 6 + (10 * 4) + (5 * 100) = 546.
В двоичном формате у нас есть только две цифры для представления числа, 0 и 1, и у нас уже закончились символы. . Так что же нам делать? Давайте применим те же правила, которые мы использовали для десятичной системы счисления.
Делаем правую цифру 0 и прибавляем 1 к левой, то есть наше следующее число — «10».Затем мы поднимаемся вверх, пока не израсходовали все наши символы с правой стороны. Итак, следующее число в строке — 11.
После «11» мы ставим 0 в обоих этих местах и прибавляем 1 слева, и получаем 100.
Затем 101, 110, 111, затем 1000…
Эта двоичная система счисления основана на двух цифрах, и каждая позиция стоит в два раза больше, чем предыдущая позиция.
Чтение двоичного числа почти такое же, как чтение десятичного. Правая цифра означает, что это означает, следующая означает два раза предыдущую, после этого 4 раза и т. Д.
Итак, 101 означает 5 в десятичной системе счисления.
Эти же правила применяются также к восьмеричной и шестнадцатеричной системам счисления. В восьмеричном формате у нас есть только 8 цифр для представления чисел, поэтому, как только мы дойдем до 7, следующим числом будет 10, а в шестнадцатеричном формате у нас будет 10 цифр и 6 букв для представления чисел. В этом случае, когда мы дойдем до 9, следующая цифра будет представлена буквой «А». Следующая буква «Б». Точно так же мы поднимаемся до буквы «F», а после «F» идет «10».
Я просто перечислю несколько чисел в этих 4 различных системах счисления и посмотрю, сможете ли вы применить правила, которые мы обсуждали выше, чтобы получить следующее число.
Чтобы понять, как компьютеры представляют положительные и отрицательные числа, прочтите это, а дополнительные сведения о шестнадцатеричном формате можно найти здесь.
Ссылки
Двоичная, шестнадцатеричная и восьмеричная системы счисления
Двоичная, шестнадцатеричная и восьмеричная системы относятся к разным системам счисления. Тот, который мы обычно используем, называется десятичным. Эти системы счисления относятся к количеству символов, используемых для представления чисел. В десятичной системе мы используем десять разных символов: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.С помощью этих десяти символов мы можем обозначить любое количество. Например, если мы видим 2, значит, мы знаем, что есть два чего-то. Например, в конце этого предложения две точки.
Когда у нас заканчиваются символы, мы переходим к размещению следующей цифры. Чтобы представить единицу больше 9, мы используем 10, что означает одну единицу из десяти и ноль единиц. Это может показаться элементарным, но очень важно понимать нашу систему счисления по умолчанию, если вы хотите понимать другие системы счисления.
Например, когда мы рассматриваем двоичную систему, в которой используются только два символа, 0 и 1, когда у нас заканчиваются символы, нам нужно перейти к размещению следующей цифры.Итак, мы будем считать в двоичном формате 0, 1, 10, 11, 100, 101 и так далее.
В этой статье более подробно рассматриваются двоичная, шестнадцатеричная и восьмеричная системы счисления и объясняется их использование.
Системы счисления используются для описания количества чего-либо или представления определенной информации. В связи с этим могу сказать, что слово «калькулятор» состоит из десяти букв. Наша система счисления, десятичная система, использует десять символов. Следовательно, десятичным считается Base Ten . Описывая системы с помощью оснований, мы можем понять, как работает эта конкретная система.
Когда мы считаем по системе Base Ten, мы считаем, начиная с нуля и заканчивая девятью по порядку.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,…
Как только мы дойдем до последнего символа, мы создадим новое размещение перед первым и посчитаем его.
8, 9, 1 0, 11, 12,…, 19, 2 0,…
Это продолжается, когда у нас заканчиваются символы для этого места размещения. Итак, после 99 мы переходим к 100.
Размещение символа указывает, сколько он стоит.Каждое дополнительное размещение дает дополнительную степень 10. Рассмотрим число 2853. Мы знаем, что это число довольно велико, например, если оно относится к количеству яблок в корзине. Это много яблок. Как мы узнаем, что он большой? Смотрим количество цифр.
Каждое дополнительное размещение — это дополнительная степень 10, как указано выше. Рассмотрим эту диаграмму.
| 10 3 | 10 2 | 10 1 | 10 0 |
|---|---|---|---|
| цифра | цифра | цифра | цифра |
| * 1000 | * 100 | * 10 | * 1 |
Каждая дополнительная цифра представляет все большее и большее количество.Это применимо как для Base 10, так и для других баз. Знание этого поможет вам лучше понять другие основы.
двоичный
Binary — это еще один способ сказать Base Two. Итак, в двоичной системе счисления для представления чисел используются только два символа: 0 и 1. Когда мы считаем с нуля в двоичной системе счисления, символы заканчиваются гораздо чаще.
Отсюда больше нет символов. Мы не переходим к 2, потому что в двоичном формате 2 не существует. Вместо этого мы используем 10.В двоичной системе 10 равно 2 в десятичной системе счисления.
Мы можем считать дальше.
| Двоичный | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Десятичное число | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Как и в десятичной системе счисления, мы знаем, что чем больше цифр, тем больше число.Однако в двоичном формате мы используем степени двойки. В двоичном числе 1001101 мы можем создать диаграмму, чтобы узнать, что это на самом деле означает.
| 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 64 + 0 + 0 + 8 + 4 + 0 + 1 | ||||||
| 77 | ||||||
Поскольку это основание два, числа не становятся такими большими, как в десятичном.Тем не менее, двоичное число из 10 цифр будет больше 1000 в десятичном.
Двоичная система используется в информатике и электротехнике. Транзисторы работают от двоичной системы, и транзисторы можно найти практически во всех электронных устройствах. 0 означает отсутствие тока, а 1 означает разрешение тока. Когда различные транзисторы включаются и выключаются, сигналы и электричество отправляются для выполнения различных действий, например для совершения звонков или вывода этих букв на экран.
Компьютеры и электроника работают с байтами или восьмизначными двоичными числами. Каждый байт содержит закодированную информацию, которую компьютер способен понять. Многие байты объединяются в цепочки для формирования цифровых данных, которые можно сохранить для дальнейшего использования.
восьмеричный
Восьмеричная система счисления — это еще одна система счисления, в которой используется меньше символов, чем в нашей традиционной системе счисления. Восьмеричный формат является модным для Base Eight, что означает, что восемь символов используются для представления всех величин. Это 0, 1, 2, 3, 4, 5, 6 и 7.Когда мы считаем единицу из 7, нам нужно новое размещение, чтобы представить то, что мы называем 8, поскольку 8 не существует в Octal. Итак, после 7 будет 10.
| восьмеричный | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12… | 17 | 20… | 30… | 77 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Десятичное число | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10… | 15 | 16… | 24… | 63 | 64 |
Так же, как мы использовали степень десяти в десятичной системе и степень двойки в двоичной системе, для определения значения числа мы будем использовать степень восьмерки, поскольку это основание восемь.Рассмотрим число 3623 по основанию восемь.
| 8 3 | 8 2 | 8 1 | 8 0 |
|---|---|---|---|
| 3 | 6 | 2 | 3 |
| 1536 + 384 + 16 + 3 | |||
| 1939 | |||
Каждое дополнительное размещение слева имеет большую ценность, чем в двоичном формате. Третья цифра справа в двоичном формате представляет только 2 3-1 , то есть 4.В восьмеричном формате это 8 3-1 , что равно 64.
Шестнадцатеричный
Шестнадцатеричная система счисления — основание шестнадцати. Как следует из основания, эта система счисления использует шестнадцать символов для представления чисел. В отличие от двоичного и восьмеричного, шестнадцатеричный имеет шесть дополнительных символов, которые он использует помимо обычных, найденных в десятичном. Но что будет после 9? 10 — это не одна цифра, а две … К счастью, по соглашению, когда необходимы дополнительные символы помимо обычных десяти, должны использоваться буквы.Итак, в шестнадцатеричном формате общий список используемых символов составляет 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. На цифровом дисплее , числа B и D строчные.
При шестнадцатеричном счете вы считаете 0, 1, 2 и так далее. Однако, когда вы достигнете 9, вы перейдете прямо к A. Затем вы считаете B, C, D, E и F. Но что дальше? У нас закончились символы! Когда у нас заканчиваются символы, мы создаем новое расположение цифр и идем дальше. Таким образом, после F будет 10. Вы продолжаете считать, пока не дойдете до 19. После 19 следующее число — 1A.Это продолжается вечно.
| Шестнадцатеричный | 9 | А | В | С | D | E | F | 10 | 11… | 19 | 1А | 1Б | 1С… | 9F | A0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Десятичное число | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 25 | 26 | 27 | 28 | 159 | 160 |
Цифры объясняются степенью 16.Рассмотрим шестнадцатеричное число 2DB7.
| 16 3 | 16 2 | 16 1 | 16 0 |
|---|---|---|---|
| 2 | D | В | 7 |
| 8192 + 3328 + 176 + 7 | |||
| 11703 | |||
Как видите, размещение в шестнадцатеричной системе счисления намного дороже, чем в любой из трех других систем счисления.
Важно знать, что 364 в восьмеричной системе счисления — это , а не , равное обычному 364.Это похоже на то, как 10 в двоичном формате определенно не является 10 в десятичном. 10 в двоичном формате (с этого момента будет записываться как 10 2 ) равно 2. 10 8 равно 8. Откуда мы это знаем? Что такое 20C.38F 16 и как нам узнать?
Вот почему важно понимать, как работают системы счисления. Используя нашу степень основного числа, становится возможным преобразовать любое число в десятичное, а из десятичного в любое.
Десятичное основание
Итак, мы знаем, что 364 8 не равно десятичному числу 364.{p-1} + … + v_1B + v_0 \ end {формула}
Где V 10 — десятичное значение, v — цифра в расположении, p — это размещение справа от числа, предполагая, что крайнее правое размещение равно 0, а B — начальная база. Не пугайтесь формулы! Мы собираемся пройти через это шаг за шагом.
Итак, допустим, у нас есть простое шестнадцатеричное число 2B. Мы хотим знать, что это за число в десятичной системе, чтобы лучше понять его. как нам это сделать?
Воспользуемся формулой выше.Сначала определите каждую переменную. Мы хотим найти V 10 , так что это неизвестно. Число 2B 16 имеет две позиции, так как оно состоит из двух цифр. Следовательно, p на единицу меньше этого значения, поэтому p равно 1. Число в базе 16, поэтому B равно 16. Наконец, мы хотим знать, что такое v, но есть несколько v. У вас v 1 и v 0 . Это относится к значению цифры в позиции индекса. v 1 относится к цифре в первой позиции (вторая цифра справа).0) \\ V_ {10} = 2 (16) +11 (1) \\ V_ {10} = 32 + 11 \ V_ {10} = 43 \\ \ end {align}
Следовательно, 2B 16 равно 43.
Теперь позвольте мне объяснить, как это работает. Помните, как расположение цифр влияет на фактическое значение? Например, в десятичном числе 123 «1» представляет 100, что составляет 1 * 10 2 . «2» — это 20 или 2 * 10 1 . Аналогично, в числе 2B 16 цифра «2» — это 2 * 16 1 , а буква B — 11 * 16 0 .
Таким образом мы можем определить значение чисел.Для числа 364 8 мы создадим диаграмму, которая показывает десятичное значение каждой отдельной цифры. Затем мы можем сложить их, чтобы получить целое. Число состоит из трех цифр, поэтому, начиная справа, у нас есть позиция 0, позиция 1 и позиция 2. Поскольку это основание восемь, мы будем использовать степень 8.
Теперь 8 2 равно 64. 8 1 равно 8. 8 0 равно 1. Что дальше?
Помните, что мы сделали с десятичным числом 123? Мы взяли значение цифры , умноженное на соответствующей мощности.Итак, учитывая это дальше…
Теперь мы складываем значения вместе, чтобы получить 244. Следовательно, 364 8 равно 244 10 .
Точно так же, как для 123, мы говорим, что есть одна группа по 100, две группы по 10 и три группы по 1, для восьмеричной системы и числа 364 существуют три группы по 64, шесть групп по 8 и четыре группы по 1.
от десятичной дроби к основанию
Так же, как мы можем преобразовать из любого основания в десятичное, можно преобразовать десятичное в любое основание.p \\ (4) \ hspace {6pt} Повторяйте шаги \ hspace {4pt} с \ hspace {4pt} 1 \ hspace {4pt} через \ hspace {4pt} 3 \ hspace {4pt}, пока \ hspace {4pt} p = 0 \\ \ end {align}
Сначала этот алгоритм может показаться запутанным, но давайте рассмотрим пример, чтобы увидеть, как его можно использовать. Мы хотим представить 236 в двоичном, восьмеричном и шестнадцатеричном формате. Итак, давайте сначала попробуем преобразовать его в двоичный код.
Первый шаг — сделать p равным $ \ operatorname {int} (\ sqrt [B] {V}) $. B — это база, в которую мы хотим преобразовать 2.V — это число, которое мы хотим преобразовать, 236. По сути, мы извлекаем квадратный корень из 236 и игнорируем десятичную часть. В результате p становится равным 7.
Шаг второй говорит, что пусть v равно нашему числу V, деленному на B p . B p равно 2 7 , или 128, а целая часть 236, деленная на 128, равна 1. Следовательно, наша первая цифра слева равна 1. Теперь мы фактически меняем V, чтобы стать V минус цифра, умноженная на В стр . Итак, V теперь будет 236-128 или 108.
Мы просто повторяем процесс до тех пор, пока p не станет равным нулю. Когда p становится равным нулю, мы завершаем шаги в последний раз, а затем заканчиваем.
Итак, поскольку V теперь равно 108, p становится 6. P \ end {уравнение}
На человеческом языке: значение шифра в числе равно значению самого шифра, умноженному на основание системы счисления в степень позиции шифра слева направо в числе, начиная с при 0.Прочтите это несколько раз и попытайтесь понять.
Таким образом, значение цифры в двоичном формате удваивается каждый раз, когда мы перемещаемся влево. (см. таблицу ниже)
Из этого следует, что каждый шестнадцатеричный шифр можно разбить на 4 двоичных разряда. На компьютерном языке: кусочек. Теперь взгляните на следующую таблицу:
| Двоичные числа | ||||||
|---|---|---|---|---|---|---|
| 8 | 4 | 2 | 1 | Шестнадцатеричное значение | Десятичное значение | |
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 0 | 2 | 2 | |
| 0 | 0 | 1 | 1 | 3 | 3 | |
| 0 | 1 | 0 | 0 | 4 | 4 | |
| 0 | 1 | 0 | 1 | 5 | 5 | |
| 0 | 1 | 1 | 0 | 6 | 6 | |
| 0 | 1 | 1 | 1 | 7 | 7 | |
| 1 | 0 | 0 | 0 | 8 | 8 | |
| 1 | 0 | 0 | 1 | 9 | 9 | |
| 1 | 0 | 1 | 0 | А | 10 | |
| 1 | 0 | 1 | 1 | В | 11 | |
| 1 | 1 | 0 | 0 | С | 12 | |
| 1 | 1 | 0 | 1 | D | 13 | |
| 1 | 1 | 1 | 0 | E | 14 | |
| 1 | 1 | 1 | 1 | F | 15 | |
Еще один интересный момент: посмотрите на значение в верхней части столбца.Тогда посмотрите на значения. Вы понимаете, о чем я? Да, ты прав! Биты включаются и выключаются в зависимости от своего значения. Значение первой цифры (начиная справа) выглядит следующим образом: 0,1,0,1,0,1,0,1,0,1,… Вторая цифра: 0,0,1,1,0 , 0,1,1,0,0,1,1,0,0… Третья цифра (значение = 4): 0,0,0,0,1,1,1,1,0,0,0,0 , 1,1,1,1,… И так далее…
А как насчет больших чисел? Поэтому нам понадобится дополнительная цифра. (но я думаю, вы догадались сами). Для значений начиная с 16 наша таблица выглядит так:
| Двоичные числа | |||||||
|---|---|---|---|---|---|---|---|
| 16 | 8 | 4 | 2 | 1 | Шестнадцатеричное значение | Десятичное значение | |
| 1 | 0 | 0 | 0 | 0 | 10 | 16 | |
| 1 | 0 | 0 | 0 | 1 | 11 | 17 | |
| 1 | 0 | 0 | 1 | 0 | 12 | 18 | |
| 1 | 0 | 0 | 1 | 1 | 13 | 19 | |
| 1 | 0 | 1 | 0 | 0 | 14 | 20 | |
| 1 | 0 | 1 | 0 | 1 | 15 | 21 | |
| 1 | 0 | 1 | 1 | 0 | 16 | 22 | |
| 1 | 0 | 1 | 1 | 1 | 17 | 23 | |
| 1 | 1 | 0 | 0 | 0 | 18 | 24 | |
| 1 | 1 | 0 | 0 | 1 | 19 | 25 | |
| 1 | 1 | 0 | 1 | 0 | 1А | 26 | |
| 1 | 1 | 0 | 1 | 1 | 1Б | 27 | |
| 1 | 1 | 1 | 0 | 0 | 1С | 28 | |
| 1 | 1 | 1 | 0 | 1 | 1D | 29 | |
| 1 | 1 | 1 | 1 | 0 | 1E | 30 | |
| 1 | 1 | 1 | 1 | 1 | 1 этаж | 31 | |
Для восьмеричных чисел это аналогично, с той лишь разницей, что нам нужно всего 3 цифры для выражения значений 1-> 7.Наша таблица выглядит так:
| Двоичные числа | |||||
|---|---|---|---|---|---|
| 4 | 2 | 1 | Восьмеричное значение | Десятичное значение | |
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 2 | 2 | |
| 0 | 1 | 1 | 3 | 3 | |
| 1 | 0 | 0 | 4 | 4 | |
| 1 | 0 | 1 | 5 | 5 | |
| 1 | 1 | 0 | 6 | 6 | |
| 1 | 1 | 1 | 7 | 7 | |
В последней теме я объяснил логику двоичной, шестнадцатеричной и восьмеричной систем счисления.Теперь я объясню кое-что более практичное. Если вы полностью поняли предыдущее, можете пропустить эту тему.
Из десятичного числа в двоичное
- Шаг 1. Убедитесь, что ваш номер нечетный или четный.
- Шаг 2: Если четный, напишите 0 (двигаясь в обратном направлении, добавляя двоичные цифры слева от результата).
- Шаг 3: В противном случае, если он нечетный, напишите 1 (таким же образом).
- Шаг 4: Разделите ваше число на 2 (отбрасывая любую дробь) и вернитесь к шагу 1. Повторяйте, пока ваше исходное число не станет 0.
Пример:
Преобразование 68 в двоичное:
- 68 четное, поэтому пишем 0.
- Разделив 68 на 2, получим 34.
- 34 тоже четное, поэтому пишем 0 (пока результат — 00)
- Разделив 34 на 2, получим 17.
- 17 нечетно, поэтому пишем 1 (результат пока — 100 — не забудьте добавить слева)
- Разделив 17 на 2, мы получим 8,5, или всего 8.
- 8 четное, поэтому пишем 0 (пока результат — 0100)
- Разделив 8 на 2, получим 4.
- 4 четное, поэтому пишем 0 (пока результат — 00100)
- Разделив 4 на 2, получим 2.
- 2 чётно, поэтому пишем 0 (результат пока — 000100)
- Разделив 2 на 2, получим 1.
- 1 нечетное, поэтому пишем 1 (пока результат — 1000100)
- Разделив на 2, мы получим 0,5 или просто 0, так что все готово.
- Конечный результат: 1000100
Из двоичного в десятичный
- Запишите значения в таблицу, как показано выше. (или мысленно)
- Добавьте значение в заголовке столбца к своему номеру, если цифра включена (1).
- Пропустить, если значение в заголовке столбца выключено (0).
- Переходите к следующей цифре, пока не закончите все.
Пример:
Преобразование 101100 в десятичное:
- Старшая цифра значения: 32. Текущий номер: 32
- Пропустите цифру «16», ее значение равно 0. Текущий номер: 32
- Добавить 8. Текущий номер: 40
- Добавить 4. Текущий номер: 44
- Пропустите цифры «2» и «1», так как их значение равно 0.
- Окончательный ответ: 44
Из десятичного в шестнадцатеричный.
ЭТО ТОЛЬКО ОДИН ИЗ МНОГИХ СПОСОБОВ!
- Преобразуйте десятичное число в двоичное
- Разделить на 4 полубайта, начиная с конца
- Посмотрите на первую таблицу на этой странице и напишите правильный номер вместо полубайта
(вы можете добавить нули в начале, если количество битов не делится на 4, потому что, как и в десятичном, это не имеет значения)
Пример:
Преобразование 39 в шестнадцатеричное:
- Сначала преобразуем в двоичный (см. Выше).Результат: 100111
- Затем мы разбиваем его на полубайты: 0010/0111 (Примечание: я добавил два нуля, чтобы прояснить тот факт, что это полубайты)
- После этого преобразуем полубайты отдельно.
- Конечный результат: 27
Из шестнадцатеричного в десятичный
* Проверьте формулу в первом абзаце и используйте ее для шифров в шестнадцатеричном числе. (это действительно работает для любого преобразования в десятичную систему счисления)
Пример:
Преобразование 1AB в десятичное:
- Значение B = 16 0 × 11.Это дает 11, очевидно,
- Значение A = 16 1 × 10. Это дает 160. Наш текущий результат — 171.
- Значение 1 = 16 2 × 1. Это дает 256.
- Конечный результат: 427
От десятичной системы к восьмеричной
- Преобразовать в двоичный.
- Разбивается на части по 3 цифры, начиная справа.
- Преобразует каждую часть в восьмеричное значение от 0 до 7
Пример: преобразовать 25 в восьмеричное
- Сначала преобразуем в двоичный.Результат: 11001
- Далее разделились: 011/001
- Преобразование в восьмеричное: 31
Из восьмеричного в десятичный
Снова применим формулу сверху
Пример: преобразовать 42 в десятичное
- Значение 2 = 8 0 × 2 = 2
- Значение 4 = 8 1 × 4 = 32
- Результат: 34
Хорошо, это может быть не на 100% «забавным», но тем не менее интересно.
- Вы склонны видеть числа, начинающиеся с 0x? Это обычная нотация для указания шестнадцатеричных чисел, поэтому вы можете увидеть что-то вроде:
0x000000
0x000002
0x000004
Эта нотация чаще всего используется для перечисления адресов компьютеров, а это совсем другая история.
- Это довольно очевидно, но вы можете «писать» слова, используя шестнадцатеричные числа. Например:
- CAB = 3243 в десятичной системе счисления.
Вы все поняли? Если вы так думаете, проверьте себя:
| Корзина | декабрь | шестигранник |
|---|---|---|
| … | … | 3A |
| … | 76 | … |
| 101110 | … | … |
| … | 88 | … |
| 1011110 | … | … |
| … | … | 47 |
Сделайте несколько упражнений самостоятельно, если хотите еще.
Двоичные, восьмеричные и шестнадцатеричные | Введение в математику колледжа
В современных вычислениях и цифровой электронике наиболее часто используются десятичные системы счисления (основание 10), двоичные (основание 2), восьмеричные (основание 8) и шестнадцатеричные (основание 16). Если мы конвертируем между двумя основаниями, отличными от десятичной, нам обычно нужно сначала преобразовать число в основание 10, а затем преобразовать это число во второе основание. Однако мы можем легко преобразовать двоичное в восьмеричное и наоборот, а также из двоичного в шестнадцатеричное и наоборот.
Это видео дает общее представление об этих преобразованиях:
Другое описание, это больше похоже на лекцию по математике:
Для дальнейшего пояснения напомним, что числа от 0 до 7 могут быть представлены до трех цифр с основанием два. В восьмерке эти числа представлены одной цифрой.
| Основание 2 (двоичное) число | Эквивалент по основанию 10 (десятичный) | База 8 (восьмеричное) число |
|---|---|---|
| 000 | 0 | 0 |
| 001 | 1 | 1 |
| 010 | 2 | 2 |
| 011 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
Теперь, когда мы дойдем до числа 8, нам понадобятся четыре цифры в базе 2 и две цифры в базе 8.Фактически, числа от 8 до 63 могут быть представлены двумя цифрами в базе 8. Нам нужны четыре, пять или шесть цифр в базе 2, чтобы представить эти же числа:
| База 2 номер | Эквивалент Base 10 | База 8 номер |
|---|---|---|
| 1000 | 8 | 10 = 1 × 8 + 0 × 1 |
| 1001 | 9 | 11 = 1 × 8 + 1 × 1 |
| 1010 | 10 | 12 = 1 × 8 + 2 × 1 |
| … | … | … |
| 111100 | 60 | 74 = 7 × 8 + 4 × 1 |
| 111101 | 61 | 75 = 7 × 8 + 5 × 1 |
| 111110 | 62 | 76 = 7 × 8 + 6 × 1 |
| 111111 | 63 | 77 = 7 × 8 + 7 × 1 |
Число 64 в базе 8 представлено как 100 8 = 1 × 8 2 + 0 × 8 1 + 0 × 8 0 = 1 × 64 + 0 × 8 + 0 × 1 .В базе 2 это будет 1000000 2 . Вы видите здесь закономерность? Для одной цифры в базе 8 нам нужно до трех цифр в базе 2. Для двух цифр в базе 8 нам нужно 4, 5 или 6 цифр в базе 2. Для трех цифр в базе 8 нам нужно 7, 8 , или 9 цифр в базе 2. Для каждой дополнительной цифры в базе 8 нам нужно до трех пробелов, чтобы представить ее в базе 2. Вот способ запомнить это: 2 3 = 8, поэтому нам нужно три пробела.
Здесь поможет пара примеров.
- Преобразуем число 6157 8 в основание 2. Мы разделяем каждую цифру в базе 8 на три цифры в базе 2, используя эквивалент из трех цифр в базе 2, поэтому 6 8 = 110 2 , 1 8 = 001 2 и т. Д.
- Преобразуйте число 10111011001010 2 в основание 8. Разделите это число на наборы по три, , начиная с самой правой цифры , затем преобразуйте каждый набор из трех в эквивалент в базе 8.
В шестнадцатеричном формате (с основанием 16) нам нужно до четырех цифр в двоичном формате для представления каждой отдельной цифры.Вспомните это, вспомнив, что 2 4 = 16, поэтому нам нужно четыре цифры.
Вы можете распечатать копии этих рабочих листов, чтобы помочь вам с преобразованием между двоичным и восьмеричным или шестнадцатеричным числами:
Если вы хотите задать себе вопрос о преобразовании чисел от 0 до 255 в двоичные, восьмеричные и шестнадцатеричные (и между этими основаниями), вот ссылка на представления этих чисел: двоичные, восьмеричные и шестнадцатеричные числа.
систем представления чисел — десятичные, двоичные, восьмеричные и шестнадцатеричные — x-engineering.org
В этой статье мы обсудим различные системы представления чисел, где они используются и почему они полезны. Вкратце мы рассмотрим представление чисел в десятичном формате , в двоичном формате , в восьмеричном формате и в шестнадцатеричном формате.
Десятичное (основание 10)
Наиболее распространенной системой представления чисел является десятичная система . Все используют это. Это настолько распространено, что большинство людей не может поверить в то, что это единственное. Его используют в финансах, инженерии и биологии почти везде, где мы видим и используем числа.
Если кто-то просит вас думать над числом, вы наверняка будете думать над десятичным числом. Если вы думаете в двоичном или шестнадцатеричном формате, вы должны иметь сильную страсть к арифметике или программному обеспечению / программированию.
Как следует из названия, десятичная система счисления использует 10 символов / знаков. В латинском языке 10 — это «decem», поэтому десятичное число может быть связано с латинским словом.
| Десятичные символы | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Как видите 9 10 символов от 0 до 9 .0 \] |
| N | … | 100000 | 10000 | 1000 | 100 | 10 | 1 | ||
В приведенном ниже примере десятичное число разбито на десятичное число Тот же метод будет применен к двоичному файлу, восьмеричная и шестнадцатеричная системы, являющиеся по сути способом преобразования числа из десятичной системы в другой формат (основание). Мы можем иметь в виду следующие характеристики десятичной системы счисления: Давайте теперь перейдем на сторону компьютерных фанатов. Другая система представления чисел - это двоичная . Как следует из названия и по аналогии с десятичной системой, мы можем сказать, что двоичная система использует только 2 символа / символа: В двоичном представлении мы используем только Двоичная система используется везде, где требуется хранить информацию в электронном формате. Все компьютеры, которые вы знаете, интеллектуальные устройства, все, что связано с электроникой и микроконтроллерами, используют двоичную систему. В электронике (цифровой) все операции выполняются с использованием двух уровней напряжения: высокого и низкого. Каждому уровню напряжения присваивается значение / символ: HIGH для 1 и LOW для 0. Для микроконтроллера, на который подается напряжение + 5 В, Примерно можно сказать, что используется двоичная система, потому что она может быть переведена в электронный сигнал. Все десятичные числа, которые мы можем придумать, можно представить в виде двоичных символов.0 \\ Как вы можете см. десятичное число Пример: Указав основание числа, мы исключаем вероятность путаницы, потому что одно и то же представление (например,грамм. 11) может означать разные вещи для разных баз. Другой способ избежать путаницы - использовать специальную нотацию (префикс) для двоичных чисел. Это потому, что Вкратце характеристики двоичной системы: Все числа в восьмеричной системе представлены с использованием 8 символов / знаков, от Шестнадцатеричная система представления чисел использует 16 символов / знаков для определения чисел.Он используется в информатике в основном потому, что может представлять большие десятичные числа с меньшим количеством символов. По сравнению с десятичной системой, здесь также используются цифровые символы от 0 до 9.0 \\ Представление десятичного числа Кратко характеристики системы представления шестнадцатеричных чисел: В таблице ниже приведены характеристики вышеупомянутые системы представления чисел. 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Системы представления восьмеричных и шестнадцатеричных чисел связаны с компьютерной системой , в основном с процессорами и микроконтроллерами.Например, если микропроцессор использует 8-битные данные, тогда восьмеричная система подходит для интерфейса данных. Если микропроцессор использует 16 бит, то для представления данных подходит шестнадцатеричная система. Есть бесконечное количество способов представить число. Десятичное число (основание 10) - это способ представления чисел большинством людей.Десятичная дробь иногда сокращается до десятичной дроби. Идет десятичный счет: Двоичный код (основание 2) - это естественный способ представления чисел и управления числами в большинстве цифровых схем. Идет двоичный счет: Восьмеричное число (с основанием 8) ранее было популярным выбором для представления номеров цифровых схем в более компактной форме, чем двоичная. Идет восьмеричный счет: Шестнадцатеричное (основание 16) в настоящее время является наиболее популярным выбором для представления номеров цифровых схем в более компактной форме, чем двоичная.(Распространенными ошибками являются «шестнадцатеричный», «шестнадцатеричный», «шестнадцатеричный» или «шестнадцатеричный».) Шестнадцатеричный счет идет: Все четыре системы счисления одинаково способны представлять любое число. На первый взгляд кажется, что использование любой другой системы счисления, кроме ориентированной на человека, является сложной и ненужной. Оказывается, способ представления числа может помочь инженеру понять значение числа в применении к цифровой схеме.Другими словами, соответствующая система счисления действительно может упростить задачу. Практически все современные цифровые схемы построены на двухпозиционных переключателях. Поскольку основной информационный элемент цифровых схем имеет два состояния, он наиболее естественно представлен системой счисления, в которой каждая отдельная цифра имеет два состояния: двоичное. Например, переключатели, которые находятся в состоянии «включено», представлены цифрой «1», а переключатели, находящиеся в состоянии «выключено», представлены цифрой «0». «Двоичная цифра» немного громоздко повторять снова и снова, поэтому термин был сокращен до «бит». Восьмеричное число (основание 8) может составлять до 1/3 длины двоичного числа (основание 2). Шестнадцатеричное число (основание 16) может составлять до 1/4 длины двоичного числа. К сожалению, десятичная дробь (основание 10) - это не целая степень двойки.Таким образом, невозможно просто разбить группы двоичных цифр на части для преобразования необработанного состояния цифровой схемы в формат, ориентированный на человека. Давайте посмотрим, как преобразовать число из двоичного ... Этот контент был заархивирован и больше не поддерживается Университетом Индианы. Информация здесь может быть неточной, а ссылки могут быть недоступны или надежны. Все данные в современных компьютерах хранятся в виде серий битов. Немного В обычном десятичном представлении (с основанием 10) каждая цифра, переходящая справа Принцип тот же самый с двоичной записью, за исключением того, что каждая цифра Поскольку двоичная запись может быть громоздкой, две более компактные записи В шестнадцатеричном формате число 42 записывается как: Знание того, представлены ли данные в восьмеричном или шестнадцатеричном формате, Это менее двусмысленный способ представления числа 42 в шестнадцатеричном формате. Примечание: Термин «двоичный», когда он используется в таких фразах, как Преобразование чисел В этом уроке по преобразованию чисел мы учимся преобразовывать числа между тремя обычно используемыми системами счисления: двоичной, восьмеричной и шестнадцатеричной. В этом руководстве мы увидим шесть примеров: Прежде чем мы начнем, давайте немного поговорим о системе счисления, которую мы собираемся рассмотреть в этом руководстве. В десятичной системе счисления мы используем десять цифр 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.Десятичная дробь подразумевает основание 10. В двоичной системе счисления мы используем две цифры 0 и 1. Двоичная означает основание 2. В восьмеричной системе счисления мы используем восемь цифр 0, 1, 2, 3, 4, 5, 6 и 7. Восьмеричная система исчисления подразумевает основание 8. В шестнадцатеричной системе счисления мы используем десять цифр и шесть букв английского алфавита 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Ниже приводится таблица преобразования, которую мы будем использовать в качестве справочной информации для выполнения операций преобразования. Чтобы преобразовать двоичное число в восьмеричное, выполните следующие действия. 2 в восьмеричную форму Чтобы преобразовать восьмеричное число в двоичное, выполните следующие шаги 8 в двоичную форму Чтобы преобразовать двоичное число в шестнадцатеричное, выполните указанные шаги. 2 в шестнадцатеричную форму Чтобы преобразовать шестнадцатеричное число в двоичное, выполните указанные шаги. 16 в двоичную форму Чтобы преобразовать восьмеричное число в шестнадцатеричное, выполните указанные шаги 8 в шестнадцатеричную форму Чтобы преобразовать шестнадцатеричное число в восьмеричное, выполните указанные шаги 16 в восьмеричное . 670. с номерами от 0 до 9 . Это просто, чтобы показать, что любое число в десятичной системе может быть разложено на сумму членов, состоящих из произведения степени 10 и символов 0… 9 .0 \\
& = 60000 & + 7000 & + 0 & + 40 & + 9
\ end {split} \ end {формула *} \] двоичная (основание 2)
0 (нули) и 1 (единицы) для представления числа. 1 (высокий) будет представлен как +5 В, а 0 (низкий). ) на 0 В.
& = 128 & + 0 & + 0 & + 16 & + 0 & + 4 & + 0 & + 1
\ end {split} \ end {формула *} \] 149 представлено в двоичной системе последовательностью нулей и единиц ( 10010101 ). Обычно, чтобы различать десятичное и двоичное число, мы должны указать основание, на которое мы ссылаемся. Основание описывается как нижний индекс после последнего символа числа Десятичное (основание 10) Двоичное (основание 2) \ [149_ {10} \] \ [10010101_ {2} \] 1100 может представлять одиннадцать сотен в десятичной системе или десятичные двенадцать в двоичной системе. Поэтому, если нужно указать двоичное число, мы используем префикс 0b . Пример: 0b1100 . Восьмеричная система (с основанием 8)
0 до 7 . 0 \\
& = 65535 & + 0 & + 1024 & + 448 & + 40 & + 1
\ end {split} \ end {формула *} \] Шестнадцатеричное (основание 16)
Шестнадцатеричные символы 0 1 2 3 4 5 6 7 9014 9014 9014 9014 9014 9014 9014 9014 9014 9014 D E F
& = 65536 & + 0 & + 1280 & + 224 & + 9
\ end {split} \ end {формула *} \] 67049 в шестнадцатеричном формате это 105E9 . Подобно двоичной системе, обычно используется префикс « 0x » для отличия от десятичной системы счисления. Пример: 0x105E9 . Система Количество символов Символы Префикс Пример Десятичный 3 10 5, 6, 7, 8, 9 Нет 147 Двоичный 2 0, 1 0b 0b10010011 Шестнадцатеричный 0144 0x 0x93 Преобразование между двоичной, восьмеричной, десятичной и шестнадцатеричной системами счисления
Четыре, которые обычно ассоциируются с современными компьютерами и цифровой электроникой: десятичная, двоичная, восьмеричная и шестнадцатеричная.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 и т. Д.
(Обычные орфографические ошибки - «bianary», «bienary» или «binery».)
Двоичные числа иногда представляются предшествующим значением "0b", как в 0b1011.
Двоичный файл иногда обозначается сокращенно как bin.
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001 и т. Д.
Octal иногда сокращается до oct.
0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20, 21 и так далее.
Шестнадцатеричные числа иногда представлены значением '0x' перед значением, как в 0x1B84.
Шестнадцатеричный код иногда сокращается как шестнадцатеричный.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11 и т. Д.
Кроме того, число может быть идеально преобразовано между различными системами счисления без потери числового значения.
Однако, поскольку работа инженеров-электриков и программистов заключается в работе с цифровыми схемами, инженерам требуются системы счисления, которые могут наилучшим образом передавать информацию между миром людей и миром цифровых схем. Элемент основной информации цифровых схем
Переключатели либо включены, либо выключены.
Не имеет значения, являются ли переключатели на самом деле физическими переключателями, электронными лампами, реле или транзисторами.
И не имеет значения, представлено ли состояние «включено» цифрой 1.8 В на новейшем ядре ЦП, -12 В на микросхеме интерфейса RS-232 или 5 В на микросхеме классической логики TTL.
Легко мгновенно понять значения 8 переключателей, представленных в двоичном виде как 10001101.Также легко построить схему для отображения каждого состояния переключателя в двоичном формате, имея светодиод (горит или не горит) для каждой двоичной цифры. Делаем ценности более компактными
Не только термин «двоичная цифра» немного громоздок, но и длина двоичного числа, поскольку каждая цифра может представлять только один переключатель.
По мере того, как цифровые схемы становились более сложными, возникла необходимость в более компактной форме представления информации о схемах.
8 - это целая степень двойки (2 3 = 8).
Это означает, что три двоичных цифры аккуратно преобразуются в одну восьмеричную цифру.
16 - это целая степень двойки (2 4 = 16).
Это означает, что четыре двоичных цифры аккуратно преобразуются в одну шестнадцатеричную цифру. Что такое двоичное, восьмеричное и шестнадцатеричное представление?
Двоичная запись
является двоичной цифрой и может иметь одно из двух значений; два значения обычно
представлены числами 0 и 1. Самая основная форма представления
компьютерные данные, таким образом, должны представлять часть данных в виде строки из единиц и нулей,
по одному на каждый бит. В итоге вы получите двоичное число или число с основанием 2; это
двоичная запись. Например, число 42 в двоичном формате будет представлено как: 101010
Интерпретация двоичной системы счисления
слева представляет собой возрастающий порядок величины (или степень десяти).В десятичной системе счисления вклад каждой следующей цифры равен десяти.
раз больше, чем предыдущая цифра. Увеличение первой цифры на
один увеличивает число, представленное на единицу, увеличивая второе
цифра на единицу увеличивает число на десять, третья цифра увеличивает
число на 100 и так далее. Число 111 на единицу меньше 112, десять
меньше 121, и сто меньше 211.
представляет собой степень двойки, превышающую предыдущую цифру, а не степень
довольно часто.Вместо цифр 1, 10, 100 и 1000 используются двоичные числа
есть 1, 2, 4 и 8. Таким образом, число два в двоичном формате будет
представлен в виде 0 в разряде единиц и 1 в разряде двойки, т. е.
10. Тройка будет 11, 1 в разряде единиц и 1 в разрядах двоек.
место. В двоичной системе счисления никогда не используется цифра больше 1. Восьмеричное и шестнадцатеричное представление
Часто используются восьмеричные и шестнадцатеричные. Восьмеричная запись представляет данные
как числа с основанием 8.Каждая цифра восьмеричного числа представляет три
биты. Точно так же в шестнадцатеричном представлении используются числа с основанием 16,
представляющие четыре бита с каждой цифрой. Восьмеричные числа используют только
цифры 0-7, в то время как шестнадцатеричные числа используют все десять цифр по основанию 10 (0-9)
и буквы a-f (представляющие числа 10-15). Число 42 - это
записывается в восьмеричном виде: 52
2а
иногда сложно (особенно если шестнадцатеричное число не использует одно из
цифры a-f), поэтому для их различения часто используется одно соглашение:
ставить «0x» перед шестнадцатеричными числами.Так вы могли бы увидеть, например: 0x2a
Вы можете увидеть пример этого использования в АРХИВИРОВАННОЙ: диаграмме сравнения наборов символов.
.
"двоичный файл" или "двоичное вложение" имеет связанный, но
немного другое значение, чем обсуждаемое здесь. Для большего
информацию см. В АРХИВИРОВАНИИ: Что такое двоичный файл? - Двоичное восьмеричное шестнадцатеричное - Преобразование - DYclassroom
1. Преобразование из двоичного в восьмеричное
2. Восьмеричное преобразование в двоичное
3. Преобразование из двоичного в шестнадцатеричное
4. Преобразование из шестнадцатеричного в двоичное
5. Восьмеричное преобразование в шестнадцатеричное
6. Шестнадцатеричное преобразование в Восьмеричное преобразование Десятичная система счисления
Двоичная система счисления
Восьмеричная система счисления
Шестнадцатеричная система счисления
10 обозначается так как A
11 обозначается как B
12 обозначается как C
13 обозначается как D
14 обозначается как E
15 обозначается как F
Шестнадцатеричная система подразумевает основание 16. Таблица преобразования
ДЕСЯТИЧНЫЙ ДВОИЧНЫЙ Восьмеричный ШЕСТИГРАННЫЙ 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 А 11 1011 13 В 12 1100 14 С 13 1101 15 D 14 1110 16 E 15 1111 17 F 1.Преобразование двоичного числа в восьмеричное
1. Разделите двоичные цифры на группы по 3 цифры, начиная справа.
2. Преобразуйте каждую группу из 3 двоичных цифр в 1 восьмеричную цифру. Преобразование двоичного числа 100101
Шаг 1. Сгруппируйте по 3 цифры справа
100101 2
Группы: 100 2 101 2
Шаг 2. Преобразуйте каждую группу из 3 цифр в 1 восьмеричную цифру.
101 2 = 5 8
100 2 = 4 8
Итак, 100101 2 = 45 8 2.Восьмеричное преобразование в двоичное
1. Преобразуйте каждую восьмеричную цифру в трехзначную двоичную группу
2. Объедините группы Преобразование восьмеричного числа 45
Шаг 1. Преобразуйте каждую восьмеричную цифру в трехзначную двоичную группу.
45 8
Группы: 4 8 5 8
5 8 = 101 2
4 8 = 100 2
Шаг 2.Объедините группы
Итак, 45 8 = 100101 2 3. Преобразование двоичного числа в шестнадцатеричное
1. Разделите двоичные цифры на группы по 4 цифры, начиная справа.
2. Преобразуйте каждую группу из 4 двоичных цифр в 1 шестнадцатеричную цифру. Преобразование двоичного числа 10100101
Шаг 1. Составьте группы по 4 цифры справа
10100101 2
Группы: 1010 2 0101 2
0101 2 = 5 16
1010 2 = 4 16
Шаг 2.Объедините группы
Итак, 10100101 2 = 45 16 4. Преобразование шестнадцатеричного числа в двоичное
1. Преобразуйте каждую шестнадцатеричную цифру в группу из 4-х цифр двоичного кода
2. Объедините группы Преобразование шестнадцатеричного числа A5
Шаг 1. Преобразуйте каждую шестнадцатеричную цифру в группу из 4-х цифр двоичного кода.
A5 16
Группы: A 16 5 16
5 16 = 0101 2
А 16 = 1010 2
Шаг 2.Объедините группы
Итак, A5 16 = 10100101 2 5. Преобразование восьмеричной системы в шестнадцатеричную
1. Преобразуйте каждую восьмеричную цифру в группы из 3-х цифр в двоичном формате
2. Объедините группы из шага 1
3. Разделите двоичные цифры из шага 2 на группы по 4 цифры , начиная справа
4. Преобразуйте каждую группу из 4 двоичных цифр в 1 шестнадцатеричную цифру. Преобразование восьмеричного числа 25
Шаг 1.Преобразуйте каждую восьмеричную цифру в группы из 3-х двоичных цифр
25 8
Группы: 2 8 5 8
5 8 = 101 2
2 8 = 010 2
Шаг 2. Объедините группы
Итак, 25 8 = 010101 2
Шаг 3. Разделите двоичные цифры из шага 2 на группы по 4 цифры, начиная справа.
Группы: 0001 2 0101 2
Шаг 4. Преобразуйте каждую группу из 4 двоичных цифр в 1 шестнадцатеричную цифру.
0101 2 = 5 16
0001 2 = 1 16
Итак, 25 8 = 15 16 6.Преобразование шестнадцатеричного числа в восьмеричное
1. Преобразуйте каждую шестнадцатеричную цифру в группы из 4-х значных двоичных
2. Объедините группы из шага 1
3. Разделите двоичные цифры из шага 2 на группы по 3 цифры , начиная справа
4. Преобразуйте каждую группу из 3 двоичных цифр в 1 восьмеричную цифру. Преобразование шестнадцатеричного числа 15
Шаг 1. Преобразуйте каждую шестнадцатеричную цифру в группы из 4-х значных двоичных чисел.
15 16
Группы: 1 16 5 16
5 16 = 0101 2
1 16 = 0001 2
Шаг 2.Объедините группы
Итак, 15 16 = 00010101 2
Шаг 3. Разделите двоичные цифры из шага 2 на группы по 3 цифры, начиная справа.
Группы: 000 2 010 2 101 2
Шаг 4. Преобразуйте каждую группу из 3 двоичных цифр в 1 восьмеричную цифру.
101 2 = 5 8
010 2 = 2 8
000 2 = 0 8
Итак, 15 16 = 025 8 = 25 8

 Binary, Octal and Hexadecimal Numbers vs Decimal Numbers
Binary, Octal and Hexadecimal Numbers vs Decimal Numbers