Ноль положительное или отрицательное: Недопустимое название | Математика | Fandom
Содержание
Почему ноль считается положительным числом, если он делитель?
Пожалуйста, проверьте следующий код.
double zero1 = 0;
double zero2 = -zero1;
bool test = zero1 == zero2; // true (1)
double number1 = 3 / zero1; // positive infinity (2)
double number2 = 3 / zero2; // negative infinity (3)
Как объяснить это противоречие? Насколько я могу судить
1 ) оно принимается как некоторое положительное малое число (например, double.Epsilon), когда оно является делителем. Но это противоречит statement (3) , так как zero2 равно нулю (и также должно приниматься как положительное малое число).
2) оно всегда принимается как некоторое положительное малое число. Это противоречит утверждению (1) (Если zero1 положительно, то zero2 должно быть отрицательно)
3) или, может быть, разделение небезопасно. Иногда
Иногда 3/0 может дать мне и отрицательную бесконечность.
Каков правильный подход, объяснение?
c#
math
Поделиться
Источник
serdar
03 ноября 2014 в 11:27
2 ответа
2
Тип Double имеет различные значения для положительного нуля и отрицательного нуля.
Когда вы сравниваете положительный ноль с отрицательным нулем, они равны. Ноль равен нулю независимо от знака.
Ноль-это точно ноль, это не очень маленькая величина. Положительный ноль и отрицательный ноль имеют одно и то же точное значение, хотя и имеют разные знаки. Если вы сравниваете очень маленькое положительное значение с очень маленьким отрицательным значением, они не равны.
Когда вы делите что-то с нулем, вы получаете положительную или отрицательную бесконечность в зависимости от знаков операндов. AFAIK, это единственная операция, где знак нуля дает другой результат. Например, использование
AFAIK, это единственная операция, где знак нуля дает другой результат. Например, использование Math.Sign для отрицательного нуля возвращает положительный ноль.
Поделиться
Guffa
03 ноября 2014 в 11:49
0
Если вам действительно не все равно, вы можете сделать это,
bool IsPositive(double value)
{
const ulong SignBit = 0x8000000000000000;
return ((ulong)BitConverter.DoubleToInt64Bits(value) & SignBit) != SignBit;
}
Поделиться
Jodrell
03 ноября 2014 в 12:40
Похожие вопросы:
Как рассчитать рост с положительным и отрицательным числом?
Я пытаюсь вычислить процентный рост в excel с положительным и отрицательным числом. This Year’s value: 2434 Last Year’s value: -2 формула, которую я использую, такова : (This_Year — Last_Year) /. ..
..
Почему отрицательный id или ноль считается плохой практикой?
Почему отрицательный идентификатор или ноль считается плохой практикой при вставке первичного ключа в таблицу базы данных? Я думаю, что это может быть полезно в некоторых случаях, но люди говорят,…
Проверьте, является ли переменная числом и положительным целым числом в PHP?
Например, скажем: <?php // Grab the ID from URL, e.g. example.com/?p=123 $post_id = $_GET[‘p’]; ?> Как проверить, является ли переменная $post_id числом, причем положительным целым числом (то…
почему я получаю «длительность должна быть положительным числом», определяя CacheProfile
У меня есть следующий метод действий:- [HttpGet] [OutputCache(CacheProfile = long, Location = OutputCacheLocation.Server, VaryByHeader = X-Requested-With)] public PartialViewResult LatestAssets() {…
В подписанных примитивах 0 является положительным или отрицательным (или и тем, и другим)?
Я читал эту страницу на Code Ranch, где говорится о переменных. Он обсуждал signed primitives, и говорил, что 0 считается отрицательным??? Я всегда думал, что 0 был положительным в этих случаях? Все…
Он обсуждал signed primitives, и говорил, что 0 считается отрицательным??? Я всегда думал, что 0 был положительным в этих случаях? Все…
почему эта переменная считается не числом
У меня есть этот код, записанный, а затем оператор println, установленный на таймере, однако все, что печатается на консоль, — это nan var songTime = CMTimeGetSeconds(player.currentTime()) Я теряюсь…
проверьте, является ли число положительным целым числом
Существует ли заранее определенная функция для проверки того, является ли число положительным целым числом? е.г 2.17 -> NO 3 -> YES В настоящее время я делаю это: if number — int(number) = 0…
Найти ноль перед любым числом в vb.net?
У меня есть эти номера 00012001, 0000012002, 012003,12004 и т. д. Если одно из этих чисел выбрано случайным образом, я хотел бы найти ноль перед числом и сохранить его в строке. Например, Если…
Почему массив с одним числом в нем считается числом?
Работая над функцией isNumeric , я обнаружил этот крайний случай: [5] считается числом, может использоваться с числовыми операторами , такими как + , — , / и т. д., и дает 5 , когда дается…
д., и дает 5 , когда дается…
как сделать -2147483648 положительным числом в Java?
Мой вопрос: как сделать -2147483648 положительным числом в Java? Мои мысли: Есть много способов сделать отрицательное число положительным: Сделайте отрицательное число положительным однако для…
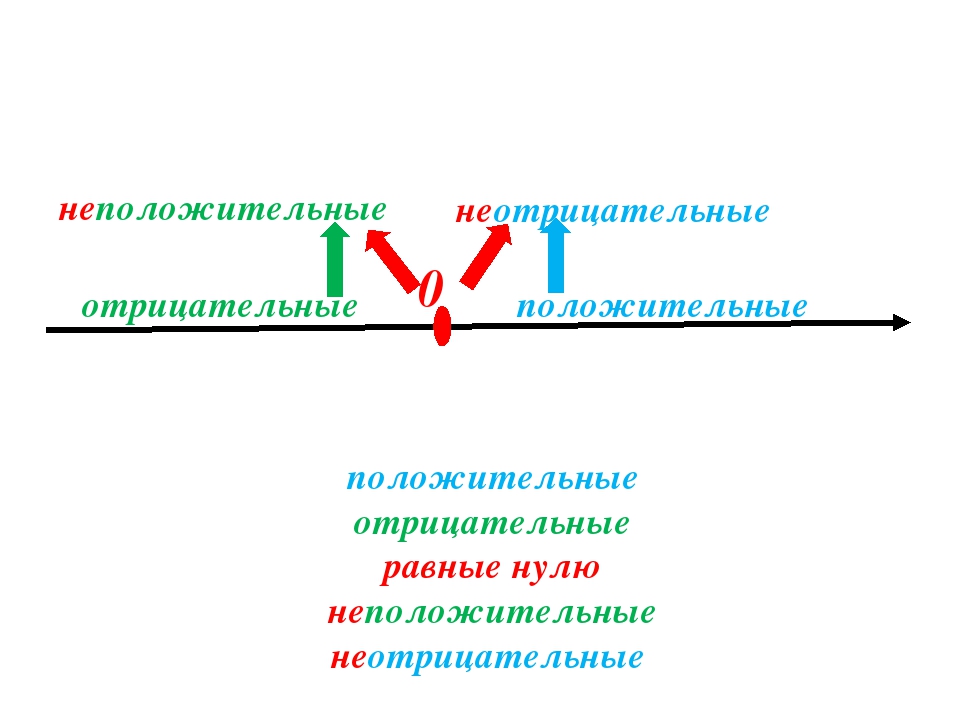
Положительные и отрицательные числа – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
По определению, положительные числа – это числа со знаком «+» перед ними (знак «+» обычно не пишут), отрицательные числа – это числа, перед которыми стоит знак «–».
Нуль не относится ни к положительным, ни к отрицательным числам. Он их разделяет.
Отрицательные числа используют для обозначения различных величин, таких как температура (ниже нуля), расход – то есть отрицательный доход, глубина – отрицательная высота и другие.
Координатная прямая – это прямая, на которой выбрано начало отсчета, указан единичный отрезок и задано направление. Число, соответствующее точке на координатной прямой, называется координатой этой точки.
Число, соответствующее точке на координатной прямой, называется координатой этой точки.
Каждому рациональному числу на числовой оси соответствует единственная точка. Рассмотрим числовую ось (рисунок внизу), обозначим на ней точку О.
Точке О поставим в соответствие число 0. Число 0 служит границей между положительными и отрицательными числами: справа от 0 – положительные числа, величина которых изменяется от 0 до плюс бесконечности, а слева от 0 – отрицательные числа, величина которых тоже изменяется от 0 до минус бесконечности.
Правило. Всякое число, стоящее на числовой оси правее, больше числа, стоящего левее.
Исходя из этого правила, положительные числа растут слева направо, а отрицательные убывают справа налево (при этом модуль отрицательного числа увеличивается).
Свойства чисел на числовой оси
- Всякое положительное число и 0 больше любого отрицательного числа.
- Всякое положительное число больше 0.
 Всякое отрицательное число меньше 0.
Всякое отрицательное число меньше 0. - Всякое отрицательное число меньше положительного числа. Положительное или отрицательное число, стоящее правее, больше положительного или отрицательного числа, стоящего левее на числовой оси.
Отрицательное число — Negative number
Действительное число, строго меньшее нуля
Этот термометр показывает отрицательную температуру по Фаренгейту (-4 ° F).
В математике , отрицательное число является вещественным числом , который меньше , чем ноль . Отрицательные числа представляют собой противоположности. Если положительное значение представляет движение вправо, отрицательное представляет движение влево. Если положительное значение соответствует уровню выше уровня моря, то отрицательное значение соответствует уровню ниже уровня моря. Если положительный результат представляет собой депозит, отрицательный — вывод средств. Они часто используются для обозначения величины потери или дефицита. Причитающийся долг можно рассматривать как отрицательный актив, уменьшение некоторого количества можно рассматривать как отрицательное увеличение. Если величина может иметь одно из двух противоположных значений, тогда можно выбрать различие между этими чувствами — возможно, произвольно — как положительное и отрицательное . Отрицательные числа используются для описания значений по шкале ниже нуля, например шкалы Цельсия и Фаренгейта для температуры. Законы арифметики для отрицательных чисел гарантируют, что здравое представление об обратном отражено в арифметике. Например, — (- 3) = 3, потому что исходное значение противоположно противоположному.
Причитающийся долг можно рассматривать как отрицательный актив, уменьшение некоторого количества можно рассматривать как отрицательное увеличение. Если величина может иметь одно из двух противоположных значений, тогда можно выбрать различие между этими чувствами — возможно, произвольно — как положительное и отрицательное . Отрицательные числа используются для описания значений по шкале ниже нуля, например шкалы Цельсия и Фаренгейта для температуры. Законы арифметики для отрицательных чисел гарантируют, что здравое представление об обратном отражено в арифметике. Например, — (- 3) = 3, потому что исходное значение противоположно противоположному.
Отрицательные числа обычно пишутся со знаком минус впереди. Например, -3 представляет собой отрицательную величину с величиной три и произносится как «минус три» или «отрицательные три». Чтобы помочь отличить операцию вычитания от отрицательного числа, иногда знак « минус» ставится немного выше знака «минус» (в виде надстрочного индекса ).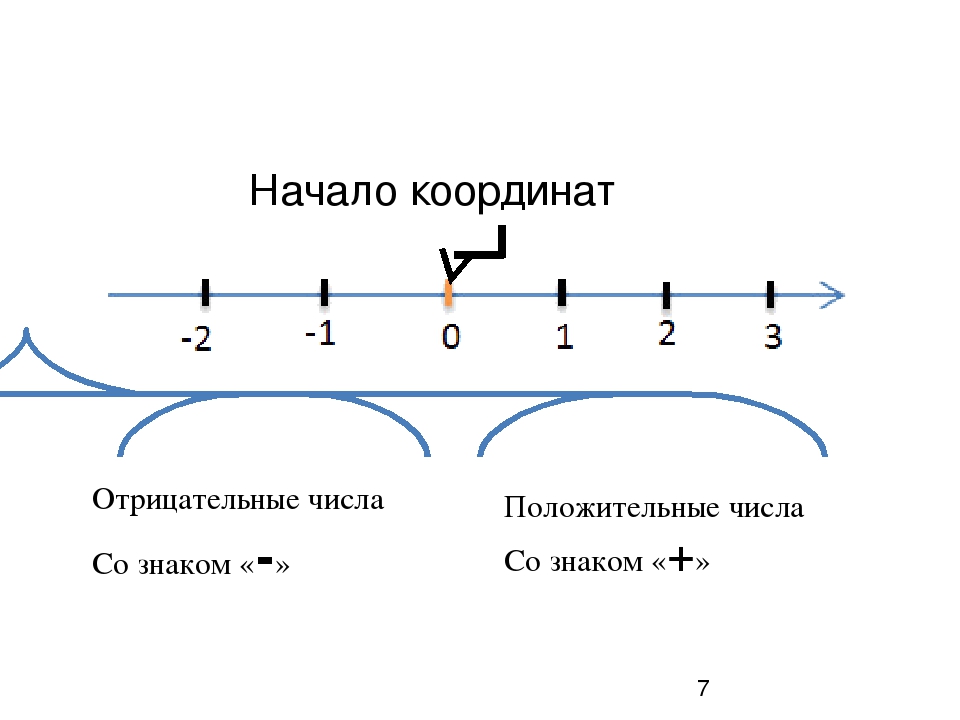 И наоборот, число больше нуля называется положительным ; ноль обычно ( но не всегда ) не считается ни положительным, ни отрицательным . Положительность числа можно подчеркнуть, поставив перед ним знак «плюс», например +3. Как правило, отрицательность или положительность числа называется его знаком .
И наоборот, число больше нуля называется положительным ; ноль обычно ( но не всегда ) не считается ни положительным, ни отрицательным . Положительность числа можно подчеркнуть, поставив перед ним знак «плюс», например +3. Как правило, отрицательность или положительность числа называется его знаком .
Каждое действительное число, кроме нуля, либо положительно, либо отрицательно. Неотрицательные целые числа называются натуральными числами (т. Е. 0, 1, 2, 3 …), а положительные и отрицательные целые числа (вместе с нулем) называются целыми числами . (Некоторые определения натуральных чисел исключают ноль.)
В бухгалтерском учете суммы задолженности часто обозначаются красными числами или числами в скобках в качестве альтернативного обозначения для представления отрицательных чисел.
Отрицательные числа впервые в истории появились в Девяти главах математического искусства , которые в нынешнем виде относятся к периоду китайской династии Хань (202 г. до н.э. — 220 г. н.э.), но вполне могут содержать гораздо более старый материал. Лю Хуэй (ок. III в.) Установил правила сложения и вычитания отрицательных чисел. К 7 веку индийские математики, такие как Брахмагупта, описывали использование отрицательных чисел. Исламские математики разработали правила вычитания и умножения отрицательных чисел и решили задачи с отрицательными коэффициентами . До появления концепции отрицательных чисел математики, такие как Диофант, считали отрицательные решения проблем «ложными», а уравнения, требующие отрицательных решений, описывались как абсурдные. Западные математики, такие как Лейбниц (1646–1716), считали отрицательные числа недействительными, но все же использовали их в расчетах.
до н.э. — 220 г. н.э.), но вполне могут содержать гораздо более старый материал. Лю Хуэй (ок. III в.) Установил правила сложения и вычитания отрицательных чисел. К 7 веку индийские математики, такие как Брахмагупта, описывали использование отрицательных чисел. Исламские математики разработали правила вычитания и умножения отрицательных чисел и решили задачи с отрицательными коэффициентами . До появления концепции отрицательных чисел математики, такие как Диофант, считали отрицательные решения проблем «ложными», а уравнения, требующие отрицательных решений, описывались как абсурдные. Западные математики, такие как Лейбниц (1646–1716), считали отрицательные числа недействительными, но все же использовали их в расчетах.
Введение
В результате вычитания
Отрицательные числа можно рассматривать как результат вычитания большего числа из меньшего. Например, отрицательное число три является результатом вычитания трех из нуля:
- 0-3 = −3.

Как правило, вычитание большего числа из меньшего дает отрицательный результат, при этом величина результата представляет собой разницу между двумя числами. Например,
- 5-8 = −3
так как 8-5 = 3 .
Числовая строка
Связь между отрицательными числами, положительными числами и нулем часто выражается в виде числовой линии :
Числа, расположенные правее в этой строке, больше, а числа, расположенные левее, меньше. Таким образом, ноль появляется посередине, положительные числа находятся справа, а отрицательные — слева.
Обратите внимание, что отрицательное число с большей величиной считается меньшим. Например, даже если (положительный) 8 больше, чем (положительный) 5 , написано
- 8> 5
отрицательный 8 считается меньше отрицательного 5 :
- −8 <−5.
(Потому что, например, если у вас есть -8 фунтов стерлингов, то есть долг в 8 фунтов стерлингов, у вас будет меньше после добавления, скажем, 10 фунтов стерлингов, чем если бы у вас было -5 фунтов стерлингов. ) Отсюда следует, что любое отрицательное число меньше, чем любое положительное число, поэтому
) Отсюда следует, что любое отрицательное число меньше, чем любое положительное число, поэтому
- −8 <5 и −5 <8.
Подписанные числа
В контексте отрицательных чисел число больше нуля называется положительным . Таким образом, любое действительное число, отличное от нуля, является положительным или отрицательным, в то время как сам ноль не считается имеющим знак. Положительные числа иногда пишутся со знаком плюс впереди, например +3 обозначает положительную тройку.
Поскольку ноль не является ни положительным, ни отрицательным, термин неотрицательный иногда используется для обозначения положительного или нулевого числа, в то время как неположительный используется для обозначения отрицательного или нулевого числа. Ноль — нейтральное число.
Повседневное использование отрицательных чисел
Спорт
Отрицательные баллы по гольфу относительно номинала.
- Разница мячей в ассоциациях футбола и хоккея ; разница очков в регби ; чистая скорость бега в крикете ; результаты игры в гольф относительно номинала .

- Плюс-минус дифференциал в хоккее : разница в общем количестве голов, забитых командой (+) и командой (-), когда конкретный игрок находится на льду, является рейтингом игрока +/–. У игроков может быть отрицательный (+/–) рейтинг.
- Дифференциал забегов в бейсболе : разница забегов отрицательна, если команда позволяет больше забегов, чем они забили.
- С клубов могут вычитаться баллы за нарушение законов, и, таким образом, у клубов может быть отрицательная сумма баллов до тех пор, пока они не заработают хотя бы такое количество баллов в этом сезоне.
- Время круга (или сектора) в Формуле 1 может быть указано как разница по сравнению с предыдущим кругом (или сектором) (например, предыдущим рекордом или кругом, только что пройденным водителем, идущим впереди), и будет положительным, если оно будет медленнее и отрицательный, если быстрее.
- В некоторых соревнованиях по легкой атлетике , таких как спринтерские гонки , преодоление препятствий , тройной прыжок и прыжок в длину , помощь от ветра измеряется и записывается и является положительной для попутного ветра и отрицательной для встречного ветра.

Наука
- Температура ниже 0 ° C или 0 ° F.
- Широта к югу от экватора и долгота к западу от нулевого меридиана .
- Топографическим характеристикам земной поверхности задается высота над уровнем моря , которая может быть отрицательной (например, отметка поверхности Мертвого моря или Долины Смерти , или отметка приливного туннеля Темзы ).
- Электрические схемы . Когда батарея подключена с обратной полярностью, считается, что приложенное напряжение противоположно ее номинальному напряжению. Например, батарея 6 (В), подключенная в обратном направлении, прикладывает напряжение -6 (В).
- Ионы имеют положительный или отрицательный электрический заряд.
- Импеданс радиовещательной башни AM, используемой в многонаправленных направленных антенных решетках, может быть положительным или отрицательным.
Финансы
- Финансовая отчетность может включать отрицательное сальдо, обозначенное знаком минус или заключением сальдо в круглые скобки.
 Примеры включают овердрафты на банковских счетах и коммерческие убытки (отрицательную прибыль ).
Примеры включают овердрафты на банковских счетах и коммерческие убытки (отрицательную прибыль ). - Возврат средств на кредитную или дебетовую карту представляет собой отрицательный заряд для карты.
- Годовой процентный рост ВВП страны может быть отрицательным, что является одним из индикаторов рецессии .
- Иногда уровень инфляции может быть отрицательным ( дефляция ), что указывает на падение средних цен.
- Ежедневное изменение в доли цен или индекс фондового рынка , такие как FTSE 100 или Dow Jones .
- Отрицательное число в финансировании является синонимом «долга» и «дефицита», которые также известны как «убыток».
- Процентные ставки могут быть отрицательными, когда кредитор должен внести свои деньги.
Другой
Отрицательная этажность в лифте.
- Нумерация этажей в доме ниже первого этажа.
- При воспроизведении аудиофайла на портативном медиаплеере , таком как iPod , на экране может отображаться оставшееся время в виде отрицательного числа, которое увеличивается до нуля с той же скоростью, что и время, которое уже воспроизведено, увеличивается с нуля.

- Телевизионные игровые шоу :
- Участники QI часто заканчивают с отрицательными баллами.
- Команды на University Challenge получают отрицательную оценку, если их первые ответы неверны и прерывают вопрос.
- Опасность! имеет отрицательный денежный балл — участники играют на определенную сумму денег, и любой неправильный ответ, который стоит им больше, чем они имеют сейчас, может привести к отрицательному баллу.
- В Цене Is Right » цены игр s купить или продать, если сумма денег теряются , что больше , чем сумма , в настоящее время в банке, он берет на себя отрицательную оценку.
- Изменение поддержки политической партии между выборами, известное как качели .
- Рейтинг одобрения политика .
- В видеоиграх отрицательное число указывает на потерю жизни, повреждение, штраф в счете или потребление ресурса, в зависимости от жанра симуляции.
- У сотрудников с гибким рабочим графиком может быть отрицательный баланс в расписании, если они отработали меньше часов, чем было по контракту к этому моменту.
 Сотрудники могут иметь возможность получать больше, чем их годовые отпускные в год, и переносить отрицательный баланс на следующий год.
Сотрудники могут иметь возможность получать больше, чем их годовые отпускные в год, и переносить отрицательный баланс на следующий год. - Транспонирование нот на электронной клавиатуре отображается на дисплее с положительными числами для увеличения и отрицательными числами для уменьшения, например, «-1» для одного полутона вниз.
Арифметика с отрицательными числами
Знак минус «-» означает оператор как для двоичного файла (двух- операнд ) операция по вычитанию (как в у — г ) и унарная (один операнд) операция отрицания (как в -x , или два раза в — ( −x) ). Частный случай унарного отрицания возникает, когда оно работает с положительным числом, и в этом случае результатом является отрицательное число (как в −5 ).
Неоднозначность символа «-» обычно не приводит к двусмысленности в арифметических выражениях, потому что порядок операций делает возможной только одну интерпретацию для каждого «-». Однако это может привести к путанице и трудностям для понимания выражения, когда символы операторов появляются рядом друг с другом. Решением может быть заключить в скобки унарный знак «-» вместе с его операндом.
Решением может быть заключить в скобки унарный знак «-» вместе с его операндом.
Например, выражение 7 + −5 может быть более ясным, если записать 7 + (−5) (даже если формально они означают одно и то же). Вычитание выражение 7-5 представляет собой другое выражение , которое не представляет собой одни и те же операции, но он оценивает к тому же результату.
Иногда в начальной школе перед числом может стоять верхний индекс минус или плюс, чтобы явно различать отрицательные и положительные числа, как в
- — 2 + — 5 дает — 7 .
Добавление
Наглядное представление сложения положительных и отрицательных чисел. Большие шары представляют собой числа с большей величиной.
Сложение двух отрицательных чисел очень похоже на сложение двух положительных чисел. Например,
- (−3) + (−5) = −8 .
Идея состоит в том, что два долга можно объединить в один долг большей величины.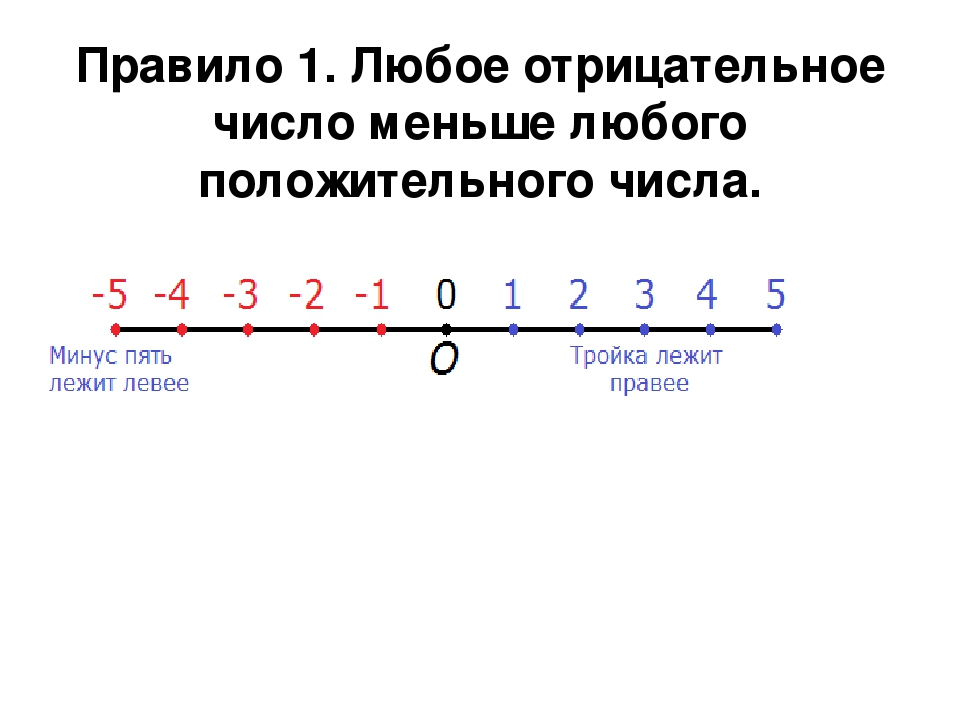
При сложении смеси положительных и отрицательных чисел можно рассматривать отрицательные числа как вычитаемые положительные величины. Например:
- 8 + (−3) = 8-3 = 5 и (−2) + 7 = 7-2 = 5 .
В первом примере кредит 8 сочетается с задолженностью 3 , что дает общий кредит 5 . Если отрицательное число имеет большую величину, результат будет отрицательным:
- (−8) + 3 = 3-8 = −5 и 2 + (−7) = 2-7 = −5 .
Здесь кредит меньше долга, поэтому чистый результат — это долг.
Вычитание
Как обсуждалось выше, вычитание двух неотрицательных чисел может дать отрицательный ответ:
- 5-8 = −3
Как правило, вычитание положительного числа дает тот же результат, что и добавление отрицательного числа равной величины. Таким образом
- 5-8 = 5 + (−8) = −3
и
- (−3) — 5 = (−3) + (−5) = −8
С другой стороны, вычитание отрицательного числа дает тот же результат, что и добавление положительного числа равной величины. (Идея состоит в том, что потеря долга — это то же самое, что и получение кредита.) Таким образом,
(Идея состоит в том, что потеря долга — это то же самое, что и получение кредита.) Таким образом,
- 3 — (−5) = 3 + 5 = 8
и
- (−5) — (−8) = (−5) + 8 = 3 .
Умножение
При умножении чисел величина продукта всегда является просто произведением двух величин. Знак продукта определяется следующими правилами:
- Произведение одного положительного числа и одного отрицательного числа отрицательно.
- Произведение двух отрицательных чисел положительно.
Таким образом
- (−2) × 3 = −6
и
- (−2) × (−3) = 6 .
Причина первого примера проста: сложение трех −2 вместе дает −6 :
- (−2) × 3 = (−2) + (−2) + (−2) = −6 .
Обоснование второго примера более сложное. Идея снова состоит в том, что потеря долга — это то же самое, что получение кредита. В этом случае потерять два долга по три штуки в каждом — это то же самое, что получить кредит в шесть:
- (-2 долга ) × (-3 каждый ) = +6 кредита.

Условие, что произведение двух отрицательных чисел является положительным, также необходимо для того, чтобы умножение соответствовало закону распределения . В этом случае мы знаем, что
- (−2) × (−3) + 2 × (−3) = (−2 + 2) × (−3) = 0 × (−3) = 0 .
Поскольку 2 × (−3) = −6 , произведение (−2) × (−3) должно равняться 6 .
Эти правила приводят к другому (эквивалентному) правилу — знак любого продукта a × b зависит от знака a следующим образом:
- если a положительно, то знак a × b такой же, как знак b , и
- если a отрицательно, то знак a × b противоположен знаку b .
Обоснование того, почему произведение двух отрицательных чисел является положительным числом, можно найти при анализе комплексных чисел .
Разделение
Знаковые правила для деления такие же, как и для умножения.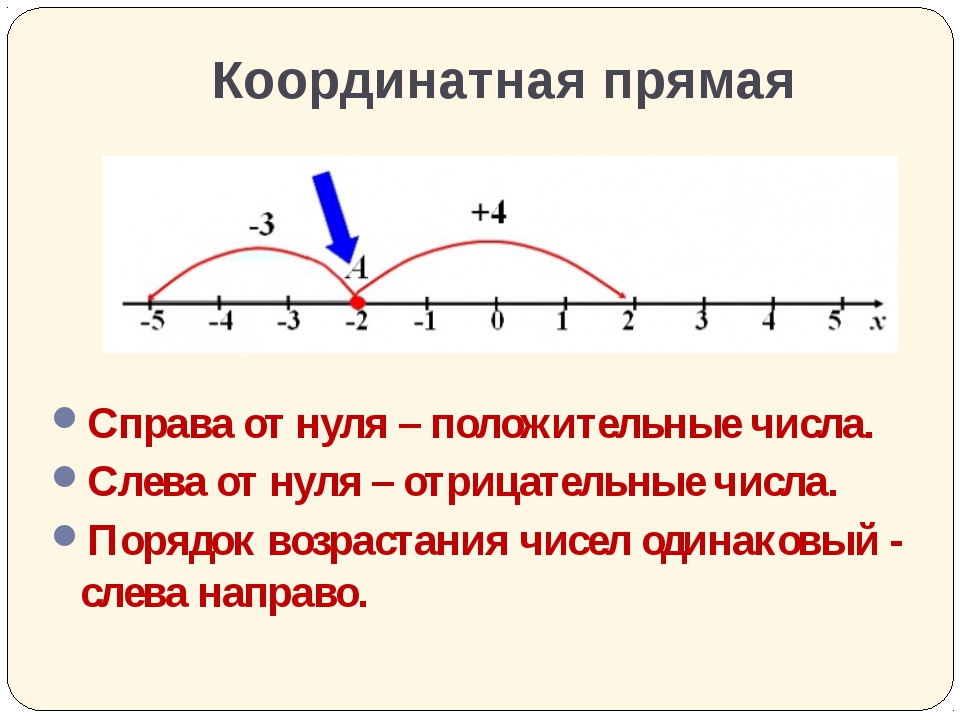 Например,
Например,
- 8 ÷ (−2) = −4 ,
- (−8) ÷ 2 = −4 ,
и
- (−8) ÷ (−2) = 4 .
Если у делимого и делителя один и тот же знак, результат будет положительным, если у них разные знаки, результат будет отрицательным.
Отрицание
Отрицательная версия положительного числа называется его отрицанием . Например, −3 — это отрицание положительного числа 3 . Сумма ряда и его отрицание равно нулю:
- 3 + (-3) = 0 .
То есть отрицание положительного числа является аддитивным обратным числом.
Используя алгебру , мы можем записать этот принцип как алгебраическое тождество :
- х + (- х ) = 0 .
Это тождество верно для любого положительного числа x . Его можно заставить действовать для всех действительных чисел, расширив определение отрицания, включив в него ноль и отрицательные числа. Конкретно:
- Отрицание 0 равно 0, и
- Отрицание отрицательного числа — соответствующее положительное число.

Например, отрицание −3 равно +3 . В целом,
- — (- х ) = х .
Абсолютное значение из числа является неотрицательным числом с той же величиной. Например, абсолютное значение −3 и абсолютное значение 3 равны 3 , а абсолютное значение 0 равно 0 .
Формальное построение отрицательных целых чисел
Подобно рациональным числам , мы можем расширить натуральные числа N до целых Z , определив целые числа как упорядоченную пару натуральных чисел ( a , b ). Мы можем расширить сложение и умножение на эти пары по следующим правилам:
- ( a , b ) + ( c , d ) = ( a + c , b + d )
- ( a , b ) × ( c , d ) = ( a × c + b × d , a × d + b × c )
Мы определяем отношение эквивалентности ~ на этих парах по следующему правилу:
- ( a , b ) ~ ( c , d ) тогда и только тогда, когда a + d = b + c .

Это отношение эквивалентности совместимо с определенными выше сложением и умножением, и мы можем определить Z как фактормножество N ² / ~, т.е. мы идентифицируем две пары ( a , b ) и ( c , d ), если они эквивалентны в выше смысла. Обратите внимание, что Z , снабженный этими операциями сложения и умножения, представляет собой кольцо и фактически является прототипом кольца.
Мы также можем определить общий порядок на Z , написав
- ( a , b ) ≤ ( c , d ) тогда и только тогда, когда a + d ≤ b + c .
Это приведет к аддитивному нулю вида ( a , a ), аддитивному инверсному к ( a , b ) виду ( b , a ), мультипликативной единице вида ( a + 1, a ) и a определение вычитания
- ( a , b ) — ( c , d ) = ( a + d , b + c ).

Эта конструкция является частным случаем конструкции Гротендика .
Уникальность
Отрицательное число уникально, как показывает следующее доказательство.
Пусть x — число, а y — его отрицательное значение. Предположим, что y ‘ — еще одно отрицательное значение x . По аксиоме действительной системы счисления
- Икс + y ′ знак равно 0 , {\ Displaystyle х + у \ прайм = 0,}
- Икс + y знак равно 0. {\ Displaystyle х + у \, \, = 0.}
Итак, x + y ‘ = x + y . Используя закон сокращения для сложения, видно, что
y ‘ = y . Таким образом, y равно любому другому отрицательному значению x . То есть y — единственный минус x .
История
Долгое время отрицательные решения проблем считались «ложными». В эллинистического Египта , в греческой математик Диофант в 3 веке нашей эры называют уравнением , которое было эквивалентно 4 х + 20 = 4 (который имеет отрицательное решение) в Arithmetica , о том , что уравнение было абсурдно. По этой причине греческие геометры могли геометрически решать все формы квадратного уравнения, дающие положительные корни; в то время как они не могли принимать во внимание других.
По этой причине греческие геометры могли геометрически решать все формы квадратного уравнения, дающие положительные корни; в то время как они не могли принимать во внимание других.
Отрицательные числа впервые в истории появляются в Девяти главах математического искусства ( Jiu zhang suan-shu ), которые в своем нынешнем виде относятся к периоду династии Хань (202 г. до н.э. — 220 г. н.э.), но могут содержать намного более старый материал. Математик Лю Хуэй (ок. III в.) Установил правила сложения и вычитания отрицательных чисел. Историк Жан-Клод Марцлофф предположил, что важность двойственности в китайской натурфилософии облегчила китайцам принятие идеи отрицательных чисел. Китайцы умели решать одновременные уравнения с отрицательными числами. В Девяти главах использовались красные счетные стержни для обозначения положительных коэффициентов и черные стержни для отрицательных. Эта система является полной противоположностью современной печати положительных и отрицательных чисел в области банковского дела, бухгалтерского учета и торговли, где красные числа обозначают отрицательные значения, а черные числа обозначают положительные значения. Лю Хуэй пишет:
Лю Хуэй пишет:
Теперь есть два противоположных вида счетных стержней для прибылей и убытков, назовем их положительными и отрицательными. Красные счетные стержни — положительные, черные — отрицательные.
В древнеиндийской рукописи Бахшали были проведены вычисления с отрицательными числами, используя «+» в качестве отрицательного знака. Дата рукописи неизвестна. Л. В. Гурджар датирует его не позднее IV века, Хорнле датирует его третьим и четвертым веками, Айангар и Пингри датируют его 8-м или 9-м веками, а Джордж Гевергезе Джозеф датирует его примерно 400 г. век
В 7 веке нашей эры отрицательные числа использовались в Индии для обозначения долгов. Индийский математик Brahmagupta , в Брахма-Sphuta-сиддханте (написано с. 630 г. н.э.), обсудили использование отрицательных чисел для получения общего вида квадратичной формулой , которая остается в использовании сегодня. Он также нашел отрицательные решения квадратных уравнений и дал правила относительно операций с отрицательными числами и нулем , например: «Долг, отрезанный от небытия, становится кредитом; кредит, отрезанный от небытия, становится долгом». Он называл положительные числа «состояниями», ноль — «цифрой», а отрицательные числа — «долгами».
Он называл положительные числа «состояниями», ноль — «цифрой», а отрицательные числа — «долгами».
В IX веке исламские математики были знакомы с отрицательными числами из работ индийских математиков, но признание и использование отрицательных чисел в этот период оставалось робким. Аль-Хорезми в своей книге «Аль-джабр ва’л-мукабала» ( отсюда и слово «алгебра») не использовал отрицательные числа или отрицательные коэффициенты. Но в течение пятидесяти лет Абу Камиль проиллюстрировал правила знаков для увеличения умножения , а аль-Караджи написал в своем аль-Фахри, что «отрицательные количества должны считаться терминами». В X веке Абу аль-Вафа аль-Бузджани рассматривал долги как отрицательные числа в «Книге о том, что необходимо из науки арифметики для писцов и бизнесменов» .
( а ± б ) ( c ± d ) {\ Displaystyle (а \ pm b) (с \ pm d)}
К XII веку преемники аль-Караджи должны были сформулировать общие правила знаков и использовать их для решения полиномиальных делений . Как пишет ас-Самав’ал :
Как пишет ас-Самав’ал :
произведение отрицательного числа — ан-наких — на положительное число — аз-азид — отрицательно, а на отрицательное число положительно. Если мы вычтем отрицательное число из большего отрицательного числа, остаток будет их отрицательной разницей. Разница останется положительной, если мы вычтем отрицательное число из меньшего отрицательного числа. Если мы вычтем отрицательное число из положительного, остаток будет их положительной суммой. Если мы вычтем положительное число из пустой степени ( martaba khāliyya ), остаток будет таким же отрицательным, а если мы вычтем отрицательное число из пустой степени, остаток будет таким же положительным числом.
В XII веке в Индии Бхаскара II дал отрицательные корни для квадратных уравнений, но отверг их, поскольку они не подходили для контекста проблемы. Он заявил, что отрицательное значение «в данном случае не следует принимать, поскольку оно неадекватно; люди не одобряют отрицательные корни».
Европейские математики по большей части сопротивлялись концепции отрицательных чисел до 17 века, хотя Фибоначчи допускал отрицательные решения финансовых проблем, где их можно было интерпретировать как дебеты (глава 13 Liber Abaci , 1202 г. н.э.), а затем как убытки (в Flos ).
В 15 веке француз Николя Шюке использовал отрицательные числа в качестве показателей, но называл их «абсурдными числами». В своей книге « Arithmetica Integra» 1544 года Майкл Стифель также имел дело с отрицательными числами, также называя их numeri absurdi .
В 1545 году Джероламо Кардано в своей книге Ars Magna впервые в Европе дал удовлетворительную трактовку отрицательных чисел. Он не допускал отрицательных чисел при рассмотрении кубических уравнений , поэтому ему пришлось рассматривать, например, x 3 + ax = b отдельно от x 3 = ax + b (с a , b > 0 в обоих случаях).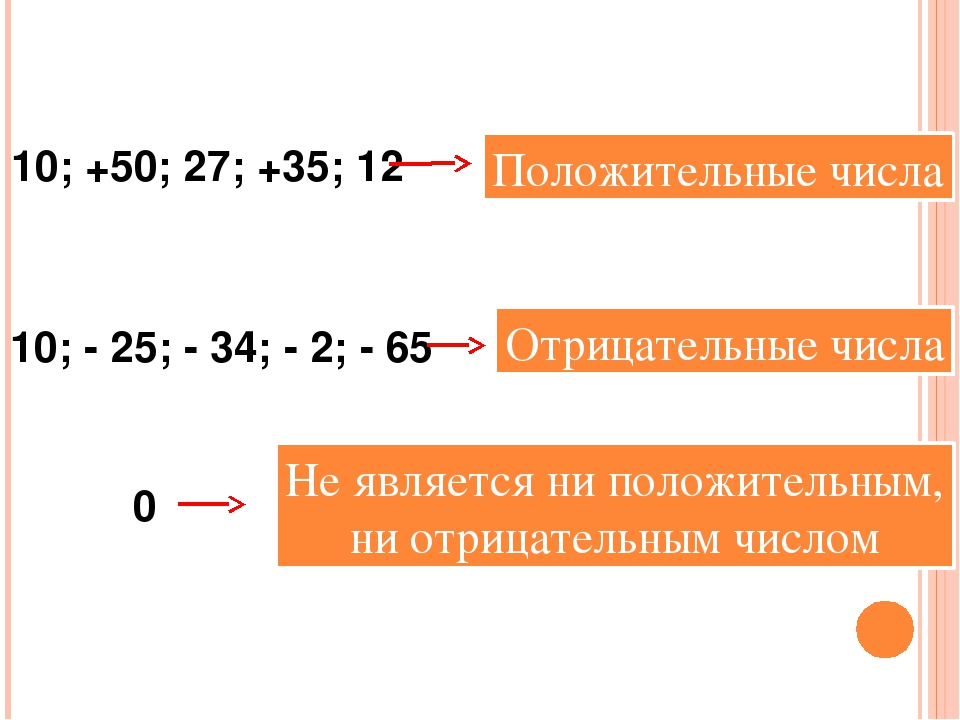 В целом Кардано был вынужден изучить тринадцать различных типов кубических уравнений, каждое из которых выражалось исключительно в терминах положительных чисел.
В целом Кардано был вынужден изучить тринадцать различных типов кубических уравнений, каждое из которых выражалось исключительно в терминах положительных чисел.
В 1759 году нашей эры английский математик Фрэнсис Масерес писал, что отрицательные числа «затемняют всю доктрину уравнений и затемняют вещи, которые по своей природе являются чрезмерно очевидными и простыми». Он пришел к выводу, что отрицательные числа бессмысленны.
В 18 веке было обычной практикой игнорировать любые отрицательные результаты, полученные из уравнений, полагая, что они бессмысленны.
Готфрид Вильгельм Лейбниц был первым математиком, который систематически использовал отрицательные числа как часть согласованной математической системы, исчисления бесконечно малых . Исчисление сделало отрицательные числа необходимыми, и их отказ от «абсурдных чисел» постепенно исчез.
Смотрите также
использованная литература
Цитаты
Список используемой литературы
- Бурбаки, Николас (1998).
 Элементы истории математики . Берлин, Гейдельберг и Нью-Йорк: Springer-Verlag. ISBN 3-540-64767-8 .
Элементы истории математики . Берлин, Гейдельберг и Нью-Йорк: Springer-Verlag. ISBN 3-540-64767-8 . - Струик, Дирк Дж. (1987). Краткая история математики . Нью-Йорк: Dover Publications.
внешние ссылки
Положительные и отрицательные числа
Натуральные числа, противоположные им числа и число 0 называются целыми числами. Положительные числа (целые и дробные), отрицательные числа (целые и дробные) и число 0 составляют группу рациональных чисел.
Рациональные числа обозначаются большой латинской буквой R. Число 0 относится к целым рациональным числам. С натуральными и дробными положительными числами мы ознакомились ранее. Рассмотрим подробнее отрицательные числа в составе рациональных чисел.
Отрицательное число с древних времен ассоциируется со словом «долг», тогда как положительное число можно ассоциировать со словами «наличие» или «доход». Значит, положительные целые и дробные числа при вычислениях — это то, что мы имеем, а отрицательные целые и дробные числа — это то, что составляет долг. Соответственно, результат вычислений — это разность между имеющимся количеством и нашими долгами.
Значит, положительные целые и дробные числа при вычислениях — это то, что мы имеем, а отрицательные целые и дробные числа — это то, что составляет долг. Соответственно, результат вычислений — это разность между имеющимся количеством и нашими долгами.
Отрицательные целые и дробные числа записываются со знаком «минус» («-») перед числом. Численная величина отрицательного числа — это его модуль. Соответственно, модуль числа — это значение числа (и положительного, и отрицательного) со знаком плюс. Модуль числа записывается так: |2|; |-2|.
Каждому рациональному числу на числовой оси соответствует единственная точка. Рассмотрим числовую ось (рисунок внизу), обозначим на ней точку О.
Точке О поставим в соответствие число 0. Число 0 служит границей между положительными и отрицательными числами: справа от 0 — положительные числа, величина которых изменяется от 0 до плюс бесконечности, а слева от 0 — отрицательные числа, величина которых тоже изменяется от 0 до минус бесконечности.
Правило. Всякое число, стоящее на числовой оси правее, больше числа, стоящего левее.
Исходя из этого правила, положительные числа растут слева направо, а отрицательные убывают справа налево (при этом модуль отрицательного числа увеличивается).
Свойства чисел на числовой оси
Всякое положительное число и 0 больше любого отрицательного числа.
Всякое положительное число больше 0. Всякое отрицательное число меньше 0.
Всякое отрицательное число меньше положительного числа. Положительное или отрицательное число, стоящее правее, больше положительного или отрицательного числа, стоящего левее на числовой оси.
Определение. Числа, которые отличаются друг от друга только знаком, называются противоположными.
Например, числа 2 и -2, 6 и -6. -10 и 10. Противоположные числа расположены на числовой оси в противоположных направлениях от точки О, но на одинаковом расстоянии от нее.
Дробные числа, представляющие собой в записи обыкновенную или десятичную дробь, подчиняются тем же правилам на числовой оси, что и целые числа. Из двух дробей больше та, которая стоит на числовой оси правее; отрицательные дроби меньше положительных дробей; всякая положительная дробь больше 0; всякая отрицательная дробь меньше 0.
Из двух дробей больше та, которая стоит на числовой оси правее; отрицательные дроби меньше положительных дробей; всякая положительная дробь больше 0; всякая отрицательная дробь меньше 0.
Например: Противоположные дроби: 0,5 и -0,5;
Как правильно умножать отрицательные числа?
Основные определения
Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.
Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:
Два главных определения:
Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.
Запоминаем!
Положительные числа — это те, что больше нуля, а отрицательные — меньшие.
Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».
Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!
Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).
Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:
Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.
Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.
Свойства умножения
|
Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор.
Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство:
А вот как умножить два числа с разными знаками:
- перемножить модули этих чисел
- перед полученным числом поставить знак минус
А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:
- «—» — при умножении минус на минус ответ будет положительным
или минус на минус дает плюс - «-+» — при умножении минуса на плюс ответ будет отрицательным
или минус на плюс дает минус - «+-» — при умножении плюса на минус ответ будет отрицательным
или плюс на минус дает минус - «++» — при умножении плюса на плюс ответ будет положительным
или плюс на плюс дает плюс.
Примеры умножения отрицательных чисел
Пример 1. Вычислить: (-2)∗(-2) и (-3)∗(-7)
Как решаем:
Вспомним правило: отрицательное число умножить на отрицательное — получается ответ со знаком плюс. Считаем:
- (-2)∗(-2) = 4
- (-3)∗(-7) = 21
Ответ: 4; 21.
Пример 2. Вычислить: (-11)∗11 и (-20)∗2
Как решаем:
Вспомним правило: отрицательное число умножить на положительное — получается ответ со знаком минус. Считаем:
- -11 * 11 = -121
- (-20) * 2 = -40
Ответ: -121; -40.
Пример 3. Вычислить произведение: 5∗(-5) и 12∗(-8)
Как решаем:
Вспомним правило: умножение положительного на отрицательное число дает отрицательный результат. Считаем:
- 5 ∗ (-5)= -25
- 12 ∗ (-8)= -96
Ответ: -25; -96.
Пример 4. Вычислить произведение: (-0,125 ) * (-6)
Как решаем:
- Используем правило умножения отрицательных чисел:
(-0,125 ) * (-6) = 0,125 * 6.
- Выполним умножение десятичной дроби на натуральное число столбиком:
Ответ: 0,75.
Развивайте математическое мышление детей на наших уроках математики вместе с енотом Максом и его друзьями. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать. Все это поможет легче и быстрее справиться со школьной математикой.
Приходите на бесплатный вводный урок вместе с ребенком: познакомимся, порешаем задачки и вдохновим на учебу!
Целые числа: положительные и отрицательные. Сравнение целых чисел
Целые числа — это положительные и отрицательные числа, не имеющие дробной части и число нуль.
Число 0 целое, но не является ни положительным, ни отрицательным числом.
Ставить перед числом нуль какой-либо знак (+ или -) не имеет смысла, так как записи
+0, -0 и 0
представляют собой одно и тоже число:
+0 = -0 = 0.
Положительные и отрицательные числа
Существуют величины, отсчёт которых производиться в двух противоположных направлениях.
Пример. Температура отсчитывается в двух противоположных направлениях от температуры тающего льда, принимаемой за нулевую:
1) Уровень ртути при нулевой температуре (температуре тающего льда).
2) Уровень ртути при температуре, более низкой, чем нулевая.
3) Уровень ртути при температуре, более высокой, чем нулевая.
Если мы имеем какую-либо величину, отсчёт которой производится в двух противоположных направлениях, то одно из направлений, безразлично какое, принято называть положительным, а другое отрицательным.
Положительное число — это число, полученное в результате измерения величины, отсчитанной в положительном направлении. Положительное число изображается в виде числа со знаком +
(плюс) впереди. Например, +16 — положительное число.
Например, +16 — положительное число.
Пример.
16 °C тепла
или +16 °C
.
Примечание: все градусы пишутся с буквой C
(Цельсия), знак градуса отделяется от числа пробелом. Например, +7 °C.
Наименьшее целое положительное число – это 1 (единица).
Отрицательное число — это число, полученное в результате измерения величины, отсчитанной в отрицательном направлении. Отрицательное число изображается в виде числа со знаком —
(минус) впереди. Например, -16 — отрицательное число.
Пример.
16 °C мороза
или -16 °C
.
Наибольшее целое отрицательное число – это -1 (минус один).
Все числа, кроме нуля, записанные со знаком +
(плюс) впереди, являются положительными, а записанные со знаком —
(минус) — отрицательными.
Пример.
+1, +15, +57 и т. д. — положительные числа;
-1, -15, -57 и т. д. — отрицательные числа.
Положительные числа можно обозначать предшествующим знаком +
(плюс) или опускать его. Числа, перед которыми не стоит знака (+ или -), считаются положительными числами. Например, вместо
+8, +14, +100 и т. д.
можно написать просто
8, 14, 100 и т. д.
Сравнение целых чисел
Сравнить два целых числа — значит, узнать, какое из них больше, какое меньше, или определить, что числа равны.
Сравнивать целые числа можно с помощью ряда целых чисел, так как числа в нём расположены от меньшего к большему, если двигаться по ряду слева направо. Поэтому в ряду целых чисел можно заменить запятые на знак меньше:
… -5 < -4 < -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 < 5 < . ..
..
Следовательно, из двух целых чисел больше то число, которое в ряду стоит правее, и меньше то, которое стоит левее, значит:
1) Любое положительное число больше нуля и больше любого отрицательного числа:
1 > 0; 15 > -16.
2) Любое отрицательное число меньше нуля:
-7 < 0; -357 < 0.
3) Из двух отрицательных чисел больше то, которое в ряду целых чисел стоит правее:
-31 < -28.
Отрицательные числа
Отрицательные числа — это числа со знаком минус (−), например −1, −2, −3. Читается как: минус один, минус два, минус три.
Примером применения отрицательных чисел является термометр, показывающий температуру тела, воздуха, почвы или воды. В зимнее время, когда на улице очень холодно, температура бывает отрицательной (или как говорят в народе «минусовой»).
Например, −10 градусов холода:
Обычные же числа, которые мы рассматривали ранее такие как 1, 2, 3 называют положительными. Положительные числа — это числа со знаком плюс (+).
Положительные числа — это числа со знаком плюс (+).
При записи положительных чисел знак + не записывают, поэтому мы и видим привычные для нас числа 1, 2, 3. Но следует иметь ввиду, что эти положительные числа выглядят так: +1, +2, +3.
Координатная прямая
Координатная прямая это прямая линия, на которой располагаются все числа: и отрицательные и положительные. Выглядит следующим образом:
Здесь показаны только числа от −5 до 5. На самом деле координатная прямая бесконечна. На рисунке представлен лишь её небольшой фрагмент.
Числа на координатной прямой отмечают в виде точек. На рисунке жирная чёрная точка является началом отсчёта. Начало отсчёта начинается с нуля. Слева от начала отсчёта отмечают отрицательные числа, а справа — положительные.
Координатная прямая продолжается бесконечно по обе стороны. Бесконечность в математике обозначается символом ∞. Отрицательное направление будет обозначаться символом −∞, а положительное символом +∞.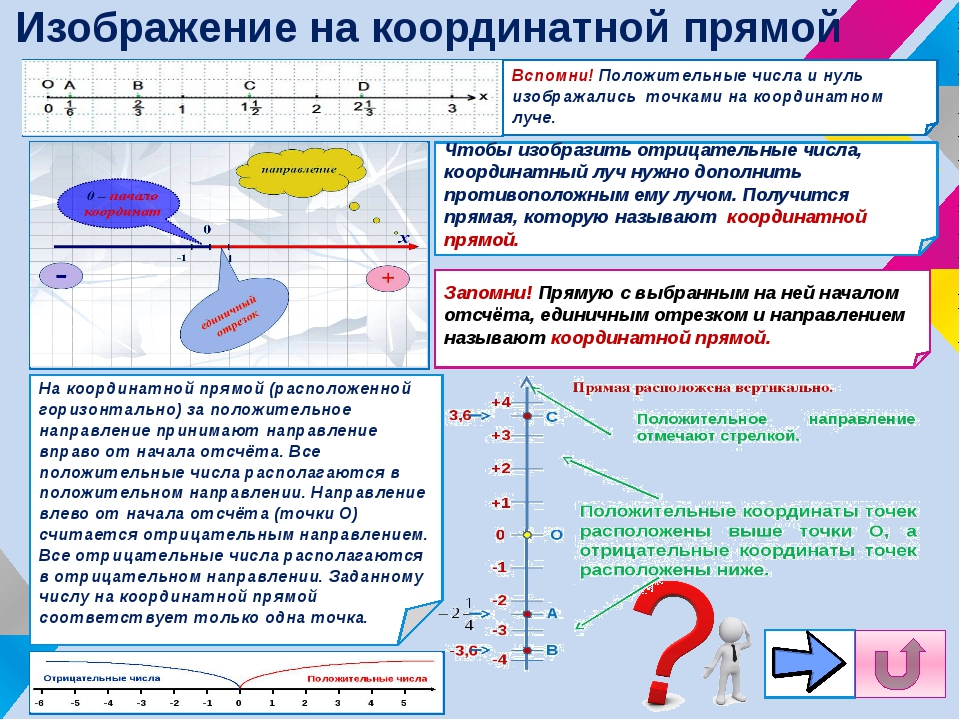 Тогда можно сказать, что на координатной прямой располагаются все числа от минус бесконечности до плюс бесконечности:
Тогда можно сказать, что на координатной прямой располагаются все числа от минус бесконечности до плюс бесконечности:
(−∞; +∞)
Каждая точка на координатной прямой имеет своё имя и координату. Имя — это любая латинская буква. Координата — это число, которое показывает положение точки на этой прямой. Проще говоря, координата это то самое число, которое мы хотим отметить на координатной прямой.
Например, точка А(2) читается как «точка А с координатой 2« и будет обозначаться на координатной прямой следующим образом:
Здесь A — это имя точки, 2 — координата точки A.
Пример 2. Точка B(4) читается как «точка B с координатой 4« и будет обозначаться на координатной прямой так:
Здесь B — это имя точки, 4 — координата точки B.
Пример 3. Точка M(−3) читается как «точка M с координатой минус три» и будет обозначаться на координатной прямой так:
Здесь M — это имя точки, −3 — координата точки M.
Точки можно обозначать любыми буквами. Но общепринято обозначать их большими латинскими буквами. Более того, начало отчёта, которое по другому называют началом координат принято обозначать большой латинской буквой O
Легко заметить, что отрицательные числа лежат левее относительно начала отсчёта, а положительные числа правее.
Существуют такие словосочетания как «чем левее, тем меньше» и «чем правее, тем больше». Наверное, вы уже догадались о чём идёт речь. При каждом шаге влево число будет уменьшаться в меньшую сторону. И при каждом шаге вправо число будет увеличиваться. Стрелка, направленная вправо, указывает на положительное направление отсчёта.
Сравнение отрицательных и положительных чисел
Правило 1. Любое отрицательное число меньше любого положительного числа.
Например, сравним два числа: −5 и 3. Минус пять меньше, чем три, несмотря на то, что пятёрка бросается в глаза в первую очередь, как цифра большая, чем три.
Связано это с тем, что −5 является отрицательным числом, а 3 — положительным. На координатной прямой можно увидеть, где располагаются числа −5 и 3
Видно, что −5 лежит левее, а 3 правее. А мы говорили, что «чем левее, тем меньше». И правило говорит, что любое отрицательное число меньше любого положительного числа. Отсюда следует, что
−5 < 3
«Минус пять меньше, чем три»
Правило 2. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой.
Например, сравним числа −4 и −1. Минус четыре меньше, чем минус единица.
Связано это опять же с тем, что на координатной прямой −4 располагается левее, чем −1
Видно, что −4 лежит левее, а −1 правее. А мы говорили, что «чем левее, тем меньше». И правило говорит, что из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. Отсюда следует, что
−4 < −1
Минус четыре меньше, чем минус единица
Правило 3. Ноль больше любого отрицательного числа.
Ноль больше любого отрицательного числа.
Например, сравним 0 и −3. Ноль больше, чем минус три. Связано это с тем, что на координатной прямой 0 располагается правее, чем −3
Видно, что 0 лежит правее, а −3 левее. А мы говорили, что «чем правее, тем больше». И правило говорит, что ноль больше любого отрицательного числа. Отсюда следует, что
0 > −3
Ноль больше, чем минус три
Правило 4. Ноль меньше любого положительного числа.
Например, сравним 0 и 4. Ноль меньше, чем 4. Это в принципе ясно и так. Но мы попробуем увидеть это воочию, опять же на координатной прямой:
Видно, что на координатной прямой 0 располагается левее, а 4 правее. А мы говорили, что «чем левее, тем меньше». И правило говорит, что ноль меньше любого положительного числа. Отсюда следует, что
0 < 4
Ноль меньше, чем четыре
Задания для самостоятельного решения
Задание 1. Сравните числа −2 и 1
Сравните числа −2 и 1
Задание 2. Сравните числа −5 и −2
Задание 3. Сравните числа −5 и −16
Задание 4. Сравните числа 15 и 20
Задание 5. Сравните числа −7 и 0
Задание 6. Сравните числа 5 и 0
Задание 7. Сравните числа 5 и 7
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Теория чисел
— Ноль положительный или отрицательный?
Я думаю, это вопрос условности. Я бы не сказал, что «неправильно» говорить о положительном значении «0», если вы с самого начала правильно определили значение «положительного».
Я не верю, что «положительное» имеет общепринятое определение значения «строго больше $ 0 $» отчасти из-за (общего) использования фразы «строго положительное число». Возможно, это слишком излишне, или это иллюстрирует тот факт, что «позитивный» не имеет общепринятого значения.
Возможно, это слишком излишне, или это иллюстрирует тот факт, что «позитивный» не имеет общепринятого значения.
Кроме того, в математике есть примеры, где использование «положительного» не имеет строгого значения. Например, функция с действительными значениями $ f: X \ rightarrow \ mathbb {R} $ обычно называется «положительной функцией», если $ f (X) \ substeq [0, \ infty) $. В теории меры обычно называют «меру» $ \ mu: \ mathcal {M} \ rightarrow [0, \ infty] $ на измеримом пространстве $ (X, \ mathcal {M}) $ «положительной мерой» ( отличить от так называемых «комплексных мер» $ \ mu: \ mathcal {M} \ rightarrow \ mathbb {C} $).В первом случае мы по-прежнему называем $ f $ положительным, даже если существуют такие $ x \ in X $, что $ f (x) = 0 $. Во втором случае мы по-прежнему называем $ \ mu $ положительным, даже если существуют такие $ E \ in \ mathcal {M} $, что $ \ mu (E) = 0 $.
В математике есть много других примеров, когда «положительный» используется для включения $ 0 $. Таким образом, по этим причинам язык либо не является общепринятым, либо вводит в заблуждение. (То есть, вводит в заблуждение в том смысле, что слово «положительный» в строгом смысле относится только к принятию о самом числе $ 0 $, а не к функциям, мерам и т. Д.?) Я также признаю, что использовать такие выражения, как «неотрицательная функция» или «неотрицательная мера», немного сложнее, чем говорить «положительная функция» или «положительная мера». Тем не менее, я думаю, что слишком быстро приходить к выводу, что неправильно рассматривать «положительное» и «неотрицательное» как синонимы. Я считаю, что это зависит от контекста.
Таким образом, по этим причинам язык либо не является общепринятым, либо вводит в заблуждение. (То есть, вводит в заблуждение в том смысле, что слово «положительный» в строгом смысле относится только к принятию о самом числе $ 0 $, а не к функциям, мерам и т. Д.?) Я также признаю, что использовать такие выражения, как «неотрицательная функция» или «неотрицательная мера», немного сложнее, чем говорить «положительная функция» или «положительная мера». Тем не менее, я думаю, что слишком быстро приходить к выводу, что неправильно рассматривать «положительное» и «неотрицательное» как синонимы. Я считаю, что это зависит от контекста.
В заключение, я думаю, что использование слова «позитивный» в строгом смысле более распространено. Но, тем не менее, использование «позитивного» в нестрогом смысле также не кажется неправильным и (осмелюсь сказать), возможно, имеет смысл в некоторых контекстах.
Как это правда, что ноль не является ни положительным, ни отрицательным числом?
Так много вопросов, которые нужно охватить, я попытаюсь ответить на каждую часть вашего вопроса, хотя и не совсем в том порядке, в котором вы ее задали.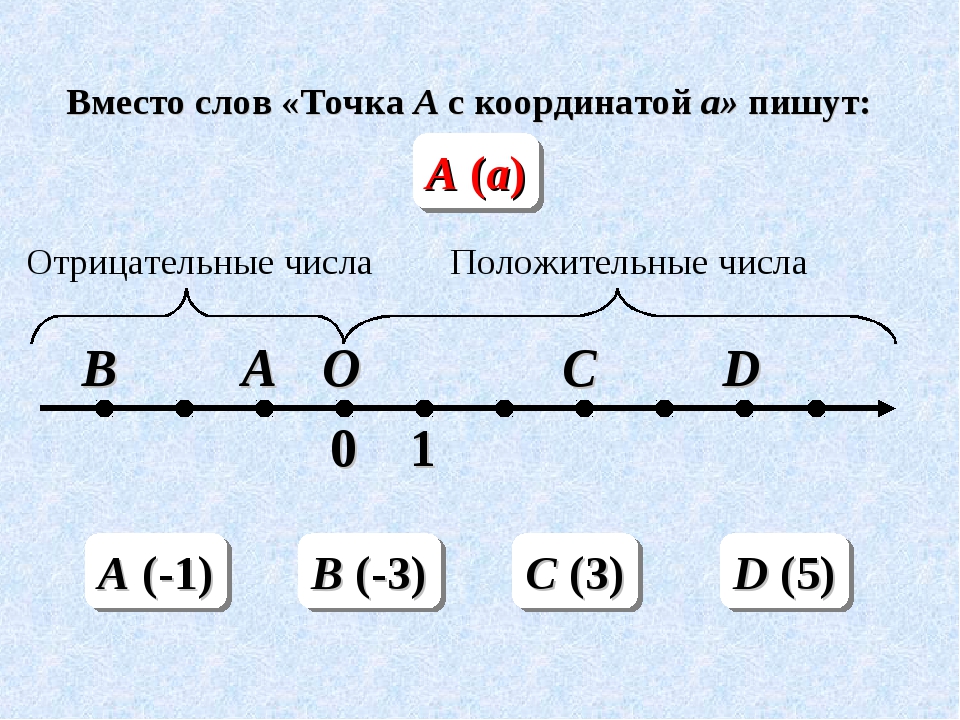
Как это правда, что ноль не является ни положительным, ни отрицательным числом?
Знаете ли вы о добавке , инвертирующей ? Определим $ f (x) $ как такое число, что $ x + f (x) = 0 $. Оказывается, $ f (x) = -1 \ times x = -x $.Аддитивное обратное положительное число — это отрицательное число. Например, аддитивная величина, обратная 8, равна $ -8 $. Аддитивное обратное отрицательное число — это положительное число. Например, аддитивный обратный к $ — \ frac {3} {2} $ равен $ \ frac {3} {2} $. Можно сказать, что $ x \ neq -x $. За исключением случая, когда $ x = 0 $, в этом случае $ -1 \ times 0 = 0 $. Это означает, что 0 является собственной аддитивной инверсией. Дело в том, что ни одно положительное число не является обратным самому себе, и никакое отрицательное число также не обладает этим свойством.
Хаген фон Эйцен уже говорил о мультипликативной перспективе, но позвольте мне расширить его точку зрения.Рассмотрим уравнение $ ax = b $. Предположим, я вам точно скажу, что такое $ a $ и $ b $. Можете ли вы определить, что такое $ x $?
- $ a = -5 $, $ b = \ frac {22} {7}
- $ a = \ sqrt {43} $, $ b = -3698 $
$
Теперь давайте немного усложним игру. Я все равно скажу вам, что такое $ b $, но вместо того, чтобы рассказывать вам, что такое $ a $, я дам вам подсказки.
- $ a $ в виде целого числа и $ a <0 $, $ b = 197 $
- $ a $ может быть целым числом и $ a \ geq 0 $, $ b = 0 $
В первом случае есть две возможности для $ x $.Но в последнем есть бесконечно много возможностей. Если $ a \ neq 0 $, то $ x $ должно быть 0. Но если $ a = 0 $, то $ x $ может быть любым, включая 0.
Сначала мне показалось, что число ноль положительное, потому что положительные числа можно писать со знаком плюс или без него слева от них … Кроме того, существует такая вещь, как $ \ pm0 $
Думайте о 0 как о точке отсчета, а о положительном — как о значении справа, а о отрицательном — как о левом (или наоборот, если хотите).$ -4 $ означает, что вы идете на 4 влево, $ + 7 $ означает 7 вправо. Таким образом, $ -0 $ означает, что вы идете на 0 влево, то есть вы остаетесь в исходной точке, и аналогично для $ + 0 $.
Однако это напоминает мне кое-что, что я где-то читал о дополнении до двух, которое сегодня используется почти во всех компьютерах. Без дополнения до двух, 0 может иметь более одного представления в виде нулей и единиц внутри компьютера, включая добросовестный $ -0 $, отличный от $ + 0 $. Но я предполагаю, что это отступление в компьютерное программирование.
, но это все еще номер, и он все еще четный.
Да, это все равно целое число, и все еще четное. Если $ m $ и $ n $ оба четные, тогда $ m — n $ также четные, верно? Что, если $ m = n $? Тогда $ m — n = 0 $. Например, 12–10 долларов = 2 доллара, а 12–14 долларов = -24 доллара, так что же будет 12–12 долларов?
Кроме того, поскольку ноль не является ни отрицательным, ни положительным, он также известен как нейтральный.
Конечно, вы можете назвать это нейтральным, и люди поймут, что вы имеете в виду, но такое использование редко встречается.
Я вижу в ваших ответах счастливые лица!
Не от меня. У меня было смущенное лицо. Я то и дело ходил между мыслями о том, что все это должно быть очевидным, и о том, что все это воспринимается как должное, но не должно быть.
чисел — целые числа со знаком — подробно
Вы
может визуализировать положительные и отрицательные целые числа, используя числовую линию.
Это важно
чтобы понять числовую строку, потому что она показывает вам, что каждое число имеет
противоположный.Знаменитый немецкий математик Леопольд Кронекер однажды сказал: «Бог
сделал положительные целые числа; все остальное — дело рук человека ».
Значит, мы путали вещи с отрицательными числами? Оказывается, там
Есть много-много повседневных проблем, в которых полезны отрицательные числа. Например,
мы можем как набрать, так и похудеть.
Температура
может подниматься или опускаться. Места на земле могут быть выше или ниже уровня моря.
уровень моря.
Целое число
целое число, которое может быть больше 0, называется положительным, или меньше
чем 0, называется отрицательным. Ноль не является ни положительным, ни отрицательным. Два целых числа
которые находятся на одинаковом расстоянии от начала координат в противоположных направлениях, называются
противоположности.
Стрелки на
каждый конец числовой линии показывает нам, что линия тянется до бесконечности в
как отрицательное, так и положительное направление. Нам не нужно включать положительный
знак (+), когда мы пишем положительные числа.Однако мы должны включить
отрицательный знак (-), когда мы пишем отрицательные числа. Ноль называется началом,
и это ни отрицательно, ни положительно.
Для каждого положительного
целое число, существует отрицательное целое число на равном расстоянии от начала координат. Два целых числа
которые находятся на одинаковом расстоянии от начала координат в противоположных направлениях, называются
противоположности. Например, «отрицательный 5» противоположен «положительному».
5. »
Каждый номер
в числовой строке также имеет абсолютное значение, что просто означает, насколько далеко
это число от нуля.Символ абсолютного значения — две вертикальные линии.
Поскольку противоположности находятся на одинаковом расстоянии от начала координат, они имеют одинаковое
абсолютная величина. Например, абсолютное значение «минус 10»
равно десяти, и абсолютное значение «положительных 10» также равно 10.
абсолютное значение нуля равно нулю.
Примеры
- 2 меньше
чем 5, потому что… 2 находится слева от 5 - -1 больше
чем -3, потому что… -1 лежит справа от -3 - -4 меньше
чем 1, потому что… -4 лежит слева от 1 - 6 больше
чем -2, потому что… 6 находится справа от -2
Что больше:
или же ?
потому что
абсолютное значение отрицательного числа противоположно.
потому что абсолютное значение положительного числа — это оно само.
51 больше
чем 13
Находят:
назад
наверх
ноль
Ноль показывает, что суммы нет.
Пример: 6-6 = 0 (разница между шестью и шестью равна нулю)
Он также используется как «заполнитель», чтобы мы могли правильно написать число.
Пример: 502 (пятьсот два) можно принять за 52 (пятьдесят два) без нуля в разряде десятков.
Ноль — это особенное число …
Он находится на полпути между -1 и +1 на числовой прямой:
.
Ноль не является ни отрицательным, ни положительным. Но это четное число.
Идея
Идея ноль , хотя и естественна для нас сейчас, не была естественной для первых людей … если нечего считать, как мы можем это считать?
Пример: можно считать собак, но нельзя считать пустое место:
| Две собаки | Zero Dogs? Ноль кошек? |
|---|
Пустой участок травы — это просто пустой участок травы!
Ноль как заполнитель
Но около 3000 лет назад людям нужно было различать такие числа, как 4 и 40. Без нуля они выглядят одинаково!
Итак, ноль теперь используется как «заполнитель»: он показывает, что «в этом месте нет числа», например:
| 502 | То есть 5 сотен, без десятков и 2 единицы |
Значение нуля
Затем люди начали думать о нуле как о фактическом числе .
Пример:
«У меня было 3 апельсина, потом я съел 3 апельсина, теперь у меня ноль апельсинов…! «
Идентификатор добавки
И у нуля есть особое свойство: когда мы добавляем его к числу, мы возвращаем это число без изменений
Пример:
7 + 0 = 7
Если сложить от 0 до 7, получим ответ 7
Также 0 + 7 = 7
Это делает его Additive Identity , что является просто особым способом сказать «добавьте 0, и мы получим , идентичный (тот же самый) номер, с которого мы начали».
Особые свойства
Вот некоторые из свойств нуля:
| Имущество | Пример |
|---|---|
| а + 0 = а | 4 + 0 = 4 |
| а — 0 = а | 4-0 = 4 |
| а × 0 = 0 | 6 × 0 = 0 |
| 0 / а = 0 | 0/3 = 0 |
| a / 0 = undefined (деление на ноль не определено) | 7/0 = не определено |
| 0 a = 0 (a положительно) | 0 4 = 0 |
| 0 0 = неопределенный | 0 0 = неопределенный |
| 0 a = undefined (a отрицательно) | 0 -2 = не определено |
| 0! = 1 («!» — факториальная функция) | 0! = 1 |
положительных и отрицательных чисел | SkillsYouNeed
Стандартные числа, любые больше нуля, называются «положительными» числами.Мы не ставим перед ними знак плюса (+), потому что в этом нет необходимости, поскольку, по общему мнению, числа без знака положительны.
Числа меньше нуля известны как «отрицательные» числа. Перед ними стоит знак минус (-), чтобы указать, что они меньше нуля (например, -10 или « минус 10 »).
Визуализация отрицательных и положительных чисел
Вероятно, самый простой способ визуализировать отрицательные и положительные числа — использовать числовую линию, инструмент, с которым вы, возможно, хорошо знакомы, особенно если у вас есть дети в начальной школе.
Это выглядит примерно так:
Числовая линия может помочь вам визуализировать как положительные, так и отрицательные числа, а также операции (сложение и вычитание), которые вы можете с ними делать.
Когда вам нужно вычислить сложение или вычитание, вы начинаете с первого числа и перемещаете второе число разрядов вправо (для сложения) или влево (для вычитания).
Эта числовая линия является упрощенной версией, но вы можете нарисовать их с любым числом, если хотите.Большим преимуществом числовой линии является то, что ее очень легко нарисовать самостоятельно на обратной стороне конверта или клочка макулатуры, а также довольно сложно ошибиться в расчетах. Если вы внимательно подсчитываете количество мест, которые вы двигаетесь, вы получите правильный ответ.
Рабочие примеры
Что такое 10-25?
Начиная с 10, вы перемещаете 25 чисел влево и сразу видите, что ответ — -15.
Что такое −17 + 23?
На этот раз вы начинаете с -17 и перемещаетесь на 23 позиции вправо. Сразу видно, что ответ — 6.
Вычитание отрицательных чисел
Если вы вычесть отрицательное число, два отрицательных числа объединятся, чтобы получить положительное.
−10 — (- 10) не равно −20. Вместо этого вы можете думать об этом как о том, чтобы повернуть один из отрицательных знаков вертикально, пересечь другой и получить плюс.Тогда сумма будет -10 + 10 = 0.
Краткое примечание по скобкам
Для наглядности, никогда нельзя писать два знака минус рядом без скобок.
Итак, если вас попросят вычесть отрицательное число, оно всегда будет заключено в скобки, чтобы вы могли увидеть, что использование двух отрицательных знаков было намеренным.
-10-10 неверно (и сбивает с толку)
-10 — (- 10) правильно (и яснее)
Умножение и деление на положительные и отрицательные числа
При умножении или делении комбинациями положительных и отрицательных чисел вы можете упростить процесс, сначала игнорируя знаки (+/-) и просто умножая или деля числа, как если бы они оба были положительными.Получив числовой ответ, вы можете применить очень простое правило для определения знака ответа:
- Когда знаки двух чисел совпадают с , ответ будет положительным .
- Если знаки двух чисел разные , ответ будет отрицательный .
Итак:
(положительное число) × (положительное число) = положительное число
(отрицательное число) × (отрицательное число) = положительное число
Но:
(положительное число) × (отрицательное число) = отрицательное число
В качестве побочного вопроса это каким-то образом объясняет, почему у вас не может быть квадратного корня из отрицательного числа (подробнее об этом читайте на нашей странице в Special Numbers and Concepts ).Квадратный корень — это число, которое умножается само на себя, чтобы получить число. Вы не можете умножить число на само по себе, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.
Правило работает точно так же, когда вам нужно умножить или разделить более двух чисел. Четное число отрицательных чисел даст положительный ответ. Нечетное количество отрицательных чисел даст отрицательный ответ.
Рабочих примеров
Что такое −5 × 25?
5 x 25 равно 125.Но здесь у вас есть одно отрицательное и одно положительное число, поэтому знак ответа будет отрицательным. Следовательно, ответ будет −125 .
Что такое −40 ÷ 8?
40 ÷ 8 равно 5. Опять же, у вас есть одно положительное и одно отрицательное число, поэтому знак ответа будет отрицательным. Ответ: −5 .
Что такое −50 ÷ −5?
50 ÷ 5 равно 10. На этот раз у вас два отрицательных числа, поэтому знак ответа будет положительным.Ответ: 10 .
Что такое −100 × −2?
100 x 2 равно 200. Опять же, у вас два отрицательных числа, поэтому ответ положительный. Это 200 .
Что такое 10 x −2 × 3?
Для начала рассмотрим первую часть расчета. 10 x 2 = 20. У вас есть одно положительное и одно отрицательное число, поэтому знак ответа будет отрицательным, то есть −20.
Теперь возьмем вторую часть вычисления: −20 × 3.Итак, 20 × 3 = 60, но опять же, у вас есть отрицательное и положительное число, поэтому ответ будет отрицательным: −60 .
Почему умножение двух отрицаний дает положительный ответ?
Тот факт, что отрицательное число, умноженное на другое отрицательное число, дает положительный результат, часто может сбивать с толку и казаться нелогичным.
Чтобы объяснить, почему это так, вспомните числовые линии, использованные ранее в этой статье, поскольку они помогают объяснить это визуально.
- Во-первых, представьте, что вы стоите на числовой прямой в нулевой точке и обращены в положительном направлении, то есть в направлении 1, 2 и так далее. Вы делаете два шага вперед, делаете паузу, затем делаете еще два шага. Вы переместились 2 × 2 шага = 4 шага.
Следовательно, положительный × положительный = положительный - Теперь вернитесь к нулю и посмотрите в отрицательном направлении, то есть в сторону −1, −2 и т. Д. Сделайте два шага вперед, затем еще два. Теперь вы стоите на −4. Вы переместились на 2 × −2 шага = −4 шага.
Следовательно, отрицательный × положительный = отрицательный
В обоих этих примерах вы двигались вперед (то есть в том направлении, куда вы смотрели), что является положительным ходом.
- Вернитесь к нулю снова, но на этот раз вы собираетесь идти назад (отрицательное движение). Снова поверните голову в положительную сторону и сделайте два шага назад. Теперь вы стоите на -2. Положительное (направление, в котором вы смотрите) и отрицательное (направление, в котором вы движетесь) приводят к отрицательному движению.
Следовательно, положительный × отрицательный = отрицательный - Наконец, снова вернемся к нулю, повернемся в отрицательном направлении. Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись в отрицательном направлении и идя назад ( два отрицательных ), вы достигли положительного результата.
Следовательно, отрицательный × отрицательный = положительный
- Два негатива компенсируют друг друга. Вы можете увидеть это в речи:
- «Просто сделай это!» положительный стимул к чему-то.
- «Не делай этого!» просит кого-то чего-то не делать. Это отрицательно.
- «Не делай этого» означает «пожалуйста». Два отрицания компенсируют и дают положительный результат как в математике, так и в речи.
- Знаки складываются физически. Когда у вас есть два отрицательных знака, один переворачивается, и они складываются, чтобы получить положительный. Если у вас есть положительный и отрицательный ответ, останется один штрих, и ответ будет отрицательным. Это простая и наглядная памятная записка, хотя она не обязательно удовлетворит тех, кто хочет понять правило.
Заключение
Отрицательные знаки могут выглядеть немного устрашающе, но правила, регулирующие их использование, просты и понятны. Помните об этом, и у вас не будет проблем.
Является ли отрицательный ноль (-0) числом в JavaScript? | Д-р Дерек Остин 🥳 | Кодирование на рассвете
Знаете ли вы, что
1 === 1 и +0 === -0 , но 1 / + 0! == 1 / -0 в JavaScript?
JavaScript имеет функцию, называемую нулями со знаком, где положительный ноль (
+0 ) совпадает с нулем без знака ( 0 ), а отрицательный ноль (-0 ) — это другое значение, хотя и ведет себя аналогичным образом. .
Фото Дэна Фримена на Unsplash
На самом деле JavaScript имеет два разных представления нуля: положительный ноль, представленный как +0 (или просто 0 ), и отрицательный ноль, представленный как -0 .
Это связано с тем, что JavaScript реализует стандарт IEEE для арифметики с плавающей запятой (IEEE 754) , в котором используются нули со знаком.
Вот как Википедия объясняет нули со знаком:
« Ноль со знаком — это ноль со связанным знаком.В обычной арифметике число 0 не имеет знака, поэтому -0, +0 и 0 идентичны.
Однако в вычислениях некоторые представления чисел допускают существование двух нулей, часто обозначаемых −0 ( отрицательный ноль ) и +0 ( положительный ноль ), которые при численном сравнении считаются равными. операции, но с возможным различным поведением в конкретных операциях.
Это происходит в представлениях чисел со знаком и величин и с дополнением до для целых чисел и в большинстве представлений чисел с плавающей запятой.
Число 0 обычно кодируется как +0, но может быть представлено как +0, так и -0 ».
Фото Мэтью Пла на Unsplash
Да, как и ожидалось, положительный ноль и отрицательный ноль равны друг другу в JavaScript, как показано в следующем примере:
Это поведение взято из раздела 7.2.13 ECMAScript, который определяет Strict Equality Алгоритм сравнения ( === ):
Сравнение
x === y, гдеxиy— значения, производит истинно или ложно .Такое сравнение выполняется следующим образом: […]4. Если x равно +0, а y равно −0, вернуть истину.
5. Если x равно -0, а y равно +0, вернуть истину.
То же самое и для алгоритма сравнения абстрактного равенства ( == ), который определен в разделе 7.2.12 ECMAScript:
Сравнение
x == y, гдеxиyявляются значениями, производит true или false .Такое сравнение выполняется следующим образом: […]3. Если Тип ( x ) совпадает с Типом ( y ), то
a. Вернуть результат выполнения строгого сравнения на равенство
x === y.
Как видите, нет никакой разницы в поведении == и === , когда оба значения имеют один и тот же тип в JavaScript.
Позже в этой статье я исследую, как различать два нуля со знаком в JavaScript, поскольку операторы равенства оценивают их как равные.
Фото Рикардо Гомеса Ангел на Unsplash
Между положительным нулем +0 и отрицательным нулем -0 в JavaScript не так много различий.
На самом деле, единственное основное отличие связано с работой с Infinity . Деление положительного числа на отрицательный ноль -0 или отрицательного числа на положительный ноль +0 даст результат -Infinity :
Кроме того, отрицательный ноль -0 генерируется делением на -Infinity. :
Это происходит потому, что отрицательный ноль -0 генерируется, когда положительный ноль +0 делится на любое отрицательное число:
В противном случае отрицательный ноль -0 довольно редко встречается в JavaScript.
Фото Жерома Пракса на Unsplash
Естественно, существование отдельного значения для нуля, которое не совсем равно нулю, вызывает некоторое недоумение. Почему стандарт IEEE должен включать два нуля?
Пользователь Агостон Хорват объясняет почему в Stack Overflow:
«Фактически, это поведение моделирует расчет пределов в математике. Например, функция 1 / x имеет значение бесконечности в 0, однако оно отделяется, если мы приближаемся к 0 с положительной или отрицательной стороны; в первом случае результат будет + inf, во втором -inf.
Но так ли должно быть? Крис Хемедингер утверждает, что такое поведение сбивает с толку в комментарии к блогу 2ality:
«Признанным недостатком IEEE-754, представления знака и величины и представления дополнения единицы является наличие двух или более представлений для нуля [0 ] ».
Некоторые другие языки программирования обходят необходимость в двух нулях, используя так называемое дополнение до двух.
Тем не менее, в JavaScript есть два разных нуля: +0 и -0 .
Фото Аарона Бёрдена на Unsplash
Используя ES6, вы можете использовать вспомогательный метод Object.is () , который различает +0 и -0 :
До ES6 единственный способ различать два нуля со знаком были путем сравнения того, производили ли они + Infinity или -Infinity :
. Также стоит отметить, что отрицательный ноль ( -0 ) также является ложным значением, что означает, что оно оценивается как ложное в Булевы выражения, как положительный ноль.
Фотография Велико Карачивиева на Unsplash
Поскольку отрицательный ноль -0 — такое редкое значение в JavaScript, его существование — это небольшая мелочь JavaScript, которая может появиться как вопрос интервью.
Тем не менее, полезно знать о нулях со знаком, если вы хотите освоить все возможности языка программирования JavaScript.
К счастью, поскольку -0 === +0 , наличие положительных и отрицательных нулей, вероятно, не является чем-то, что вызовет ошибки или ошибки в вашем коде!
Но, если вам нужно отличить отрицательный ноль -0 от положительного нуля +0 , это легко сделать с помощью метода сравнения ES6 Object.это () .
Фото Криса Лю-Бирса на Unsplash Фото Рикардо Гомеса Ангела на Unsplash
Правила положительных и отрицательных чисел
Положительные и отрицательные числа — это два широких класса чисел, которые используются в математике, а также в повседневных транзакциях, таких как управление деньгами или измерение веса .
- Положительное число имеет значение больше нуля. Его знак положительный, но обычно он пишется без знака плюса перед ним (например, 4, 51, а не +4, +51).
- Отрицательное число имеет значение меньше нуля.Его знак считается отрицательным и пишется со знаком минус перед ним (например, -2, -23).
- Сумма положительного числа и равного ему отрицательного числа равна нулю.
- Ноль не является ни положительным, ни отрицательным числом.
Существуют правила сложения, вычитания, умножения и деления положительных и отрицательных чисел. Как правило, легче выполнять операции с отрицательными числами, если они заключены в квадратные скобки, чтобы разделять их. Числовые линии также упрощают понимание положительных чисел и чисел.
Сложение и вычитание положительных и отрицательных чисел
Когда вы складываете или вычитаете положительные и отрицательные числа, знак ответа зависит от того, похожи ли знаки или какое число имеет большее значение.
Сложить положительные и отрицательные числа просто, если оба числа имеют одинаковый знак. Просто найдите сумму чисел и держите знак. Например:
- 3 + 2 = 5
- (-4) + (-2) = -6
Найдите сумму положительного и отрицательного числа, вычтя число с меньшим значением из числа с большее значение.Знак — это знак большего числа.
- (-7) + 2 = -5
- 4 + (-8) = 4-8 = -4
- (-3) + 8 = 5
- 10 + (-2) = 10-2 = 8
- (-5) + 4 = -1
Правила вычитания аналогичны правилам сложения. Для двух положительных чисел, если первое число больше второго, результатом будет другое положительное число.
Если вы вычтите большое положительное число из меньшего положительного числа, вы получите отрицательное число.
Легкий способ сделать это — вычесть меньшее число из большего числа и изменить знак ответа на минус.
Когда вы вычитаете положительное число из отрицательного числа, это то же самое, что прибавлять отрицательное число. Другими словами, это делает отрицательное число более отрицательным.
- (-4) — 3 = (-4) + (-3) = -7
- (-10) — 12 = (-10) + (-12) = -24
Вычитание отрицательного числа из положительного числа отменяет отрицательные знаки и становится простым сложением.Это делает положительное число более положительным.
- 4 — (-3) = 4 + 3 = 7
- 5 — (-2) = 5 + 2 = 7
Когда вы вычитаете отрицательное число из другого отрицательного числа, отрицательные знаки снова отменяют каждое другое, чтобы стать знаком плюс. Ответ имеет знак большего числа.
- (-2) — (-7) = (-2) + 7 = 5
- (-5) — (-3) = (-5) + 3 = -2
Умножение и деление положительного и отрицательные числа
Если вы умножите или разделите одинаковые знаки, вы получите положительное число.Умножение или деление положительных и отрицательных чисел дает отрицательное число.
Правила умножения и деления просты:
- Если оба числа положительны, результат будет положительным.
- Если оба числа отрицательны, результат положительный. (По сути, два отрицательных значения компенсируют друг друга).
- Если одно число положительное, а другое отрицательное, результат будет отрицательным.
- Если вы умножаете или делите несколько чисел знаками, сложите количество положительных и отрицательных чисел.

 Всякое отрицательное число меньше 0.
Всякое отрицательное число меньше 0.


 Примеры включают овердрафты на банковских счетах и коммерческие убытки (отрицательную прибыль ).
Примеры включают овердрафты на банковских счетах и коммерческие убытки (отрицательную прибыль ).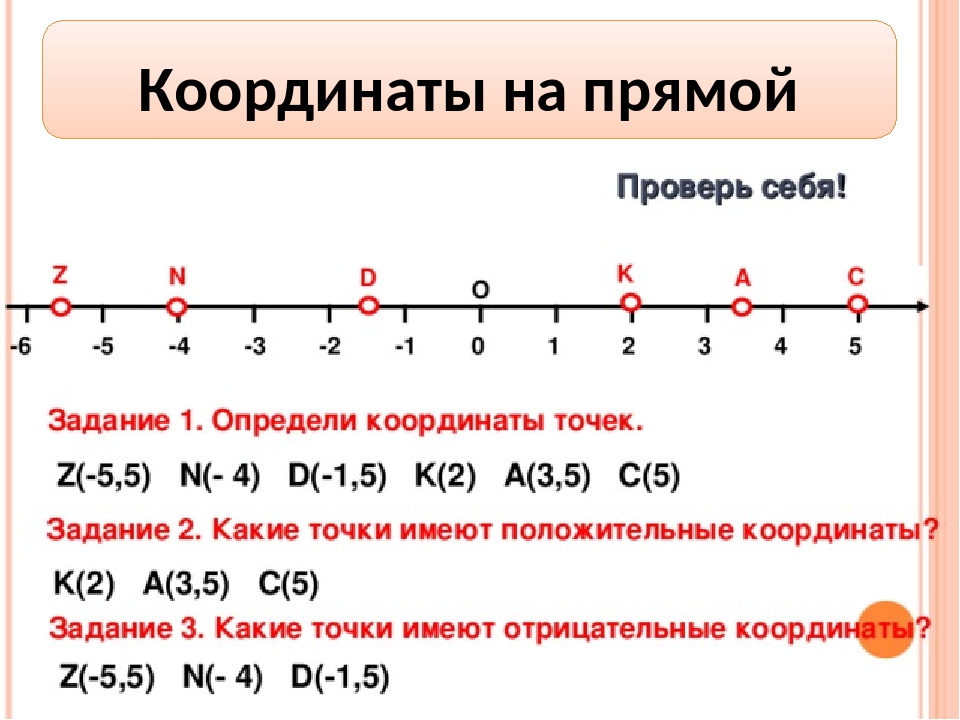
 Сотрудники могут иметь возможность получать больше, чем их годовые отпускные в год, и переносить отрицательный баланс на следующий год.
Сотрудники могут иметь возможность получать больше, чем их годовые отпускные в год, и переносить отрицательный баланс на следующий год.
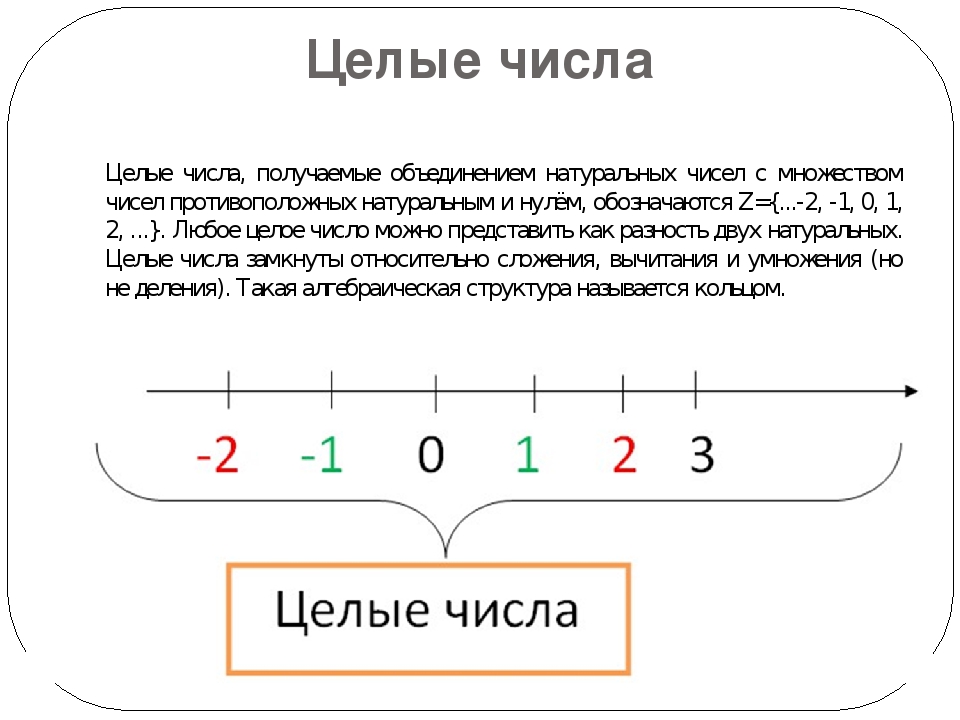 Элементы истории математики . Берлин, Гейдельберг и Нью-Йорк: Springer-Verlag. ISBN 3-540-64767-8 .
Элементы истории математики . Берлин, Гейдельберг и Нью-Йорк: Springer-Verlag. ISBN 3-540-64767-8 .