Отрицательные числа: Сложение и вычитание отрицательных и положительных чисел. Решение примеров.
Содержание
Сложение и вычитание отрицательных и положительных чисел. Решение примеров.
Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.
Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:
- Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.
\((-2)+(-3)=-5\)
- Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:
\((-8)+4=4-8=-4\)
\(9+(-4)=9-4=5\)
Для каждого числа кроме \(0\) существует противоположный элемент, при сумме с ним образуется ноль:
\(-9+9=0\) \(7,1+(-7,1)=0\)
- При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс.
 То есть, если стоят рядом два минуса, в сумме получается плюс.
То есть, если стоят рядом два минуса, в сумме получается плюс.
\((-7)-(-6)=(-7)+6=(-1)\)
- Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.
\(7-9=-2\) так как \(9>7\)
- Также не стоит забывать минус на минус дает плюс:
\(7-(-9)=7+9=16\)
Задача 1. Вычислите:
- \(4+(-5)\)
- \(-36+15\)
- \((-17)+(-45)\)
- \(-9+(-1)\)
Решение:
- \(4+(-5)=4-5=-1\)
- \(-36+15=-21\)
- \((-17)+(-45)\) \(=-17-45=-62\)
- \(-9+(-1)=-9-1=-10\)
Задача 2. Вычислите:
- \(3-(-6)\)
- \(-16-35\)
- \(-27-(-5)\)
- \(-94-(-61)\)
Решение:
- \(3-(-6)=3+6=9\)
- \(-16-35=-51\)
- \(-27-(-5)=-27+5=-22\)
- \(-94-(-61)=-94+61=-33\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Положительные и отрицательные числа
Можно ли из меньшего числа вычесть большее? Рассмотрение этого вопроса мы начали в предыдущей статье.
Для того чтобы прояснить ситуацию, нарисуем вертикальную линию и отметим на ней точкой положение города. Эту точку мы будем считать точкой отсчета или нулем. Теперь нанесем на прямую по несколько равных делений выше и ниже нулевой точки. Пусть каждое деление соответствует одному километру.
Числа выше точки отсчета (то есть к северу от города) будем называть обычными (или положительными), а числа ниже точки отсчета (то есть к югу от города) будем называть числами, меньшими нуля, или отрицательными.
Теперь нам понадобится специальный символ, который поможет различить положительные и отрицательные числа. Обычно для этого используют систему обозначений, основанную на способе, которым можно получить это число. Любое положительное число получается в результате сложения других положительных чисел. Символом сложения является знак «+», поэтому положительные числа обозначаются +1, +2, +3 и так далее. Само название «положительное число» говорит о том, что это число реально существует.
Отрицательные числа получаются как результат вычитания, скажем, при вычитании (2-3) мы получаем число на единицу меньше нуля. Его обозначают -1. Таким образом, отрицательные числа обозначают — -1, -2, -3, и так далее.
То, что числа, меньшие нуля, получили название отрицательных, не случайно. Даже когда математики освоили операции с числами, меньшими нуля, надо было подчеркнуть, что эти числа не существуют в действительности.
Обратите внимание, ноль не является ни положительным, ни отрицательным числом.
Теперь у нас вертикальная размеченная линия, то есть шкала, и мы можем использовать ее для операций сложения и вычитания. Поскольку положительные числа увеличиваются вверх по шкале, а операции сложения положительных чисел приводят к увеличению чисел, будем считать, что сложение – это движение вверх по шкале. Вычитание – это операция, противоположная сложению, поэтому вычитание – это движение вниз по шкале.
Предположим, надо сложить +2 и +5. Записать это выражение можно следующим образом: (+2) + (+5). Скобки нам понадобились по той причине, что необходимо отделить плюс как знак операции сложения от плюсов, обозначающих положительные числа. Но поскольку мы привыкли к тому, что обычно имеем дело с положительными числами, то часто знаки «+» перед положительными числами просто опускают. Тогда получаем: 2+5. Необходимо ставить знаки «+» перед положительными числами только в тех случаях, когда надо привлечь особое внимание к знаку числа.
Теперь отложим на нашей шкале два деления вверх. Это число 2. Прибавим еще 5 делений и остановимся на делении 7, то есть 2+5=7. Мы можем начать с 5 и прибавить два деления. Мы опять получим 7. Тут я еще раз хочу обратить ваше внимание на тот факт, что от перемены мест слагаемых сумма не меняется.
Это число 2. Прибавим еще 5 делений и остановимся на делении 7, то есть 2+5=7. Мы можем начать с 5 и прибавить два деления. Мы опять получим 7. Тут я еще раз хочу обратить ваше внимание на тот факт, что от перемены мест слагаемых сумма не меняется.
Теперь займемся вычитанием. Предположим, надо вычесть 2 из 5. От точки 5 на шкале мы откладываем вниз два деления и оказываемся в точке 3. Таким образом, получаем 5-2=3.
Теперь нам надо выяснить, как обращаться с отрицательными числами. Можно ли производить с ними такие же действия, как и с положительными числами? Если да, то они окажутся очень полезными, несмотря на то что не являются «настоящими» числами. И действительно, отрицательные числа нашли широчайшее применение не только в науке и инженерной практике, но и в повседневной деятельности. Они применяются, например, в бухгалтерии, где запасы и доходы обозначаются положительными числами, а расходы – отрицательными.
Материалы по теме:
Поделиться с друзьями:
Загрузка. ..
..
Отрицательные числа
Главная /
Ассемблер /
Для чайников /
Введение /
Представление данных /
Мы разобрались, как в памяти компьютера представлены
положительные числа,
то есть числа без знака. Но ведь числа бывают и отрицательными, то есть числа со знаком минус.
Чтобы применять те же самые байты и слова для представления отрицательных чисел,
существует специальная операция, которая называется
дополнение до двух. Но прежде чем рассмотреть эту операцию, покажем,
как отрицательное число отличить от положительного.
Для того чтобы указать знак числа, достаточно одного разряда (бита). Обычно знаковый бит
занимает старший разряд числа. Если старший бит числа равен 0, то число считается положительным.
Если старший разряд числа равен 1, то число считается отрицательным. Пример байта со знаком
приведён на рис. 2.3.
| Разряды | Число | |||||||
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | -110 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | +110 |
Рис. 2.3. Отрицательное число в памяти компьютера.
2.3. Отрицательное число в памяти компьютера.
Как вы успели заметить, для представления числа со знаком требуется использовать старший
бит для определения знака числа. Это означает, что этот старший бит уже нельзя
использовать для записи самого числа, то есть максимальное значение, которое мы сможем
записать в байт, будет уже не 255, а всего 127. Диапазоны возможных значений чисел
со знаком приведены в таблице 2.5.
Таблица 2.5. Диапазоны возможных значений чисел со знаком.
| Тип числа | Диапазон значений | Степени двойки |
| Байт | –128…+127 | -27…(27 – 1) |
| Слово | –32 768…+32 767 | -215…(215 – 1) |
| Двойное слово | –2 147 483 648… +2 147 483 647 | -231…(231 – 1) |
| Учетверённое слово | –9 223 372 036 854 775 808… +9 223 372 036 854 775 807 | -263…(263 – 1) |
А теперь разберёмся с загадочной операцией дополнение до двух.
Для изменения знака числа выполняется инверсия, то есть для числа
в двоичном представлении все нули заменяются единицами, а все единицы – нулями.
Затем к полученному результату прибавляют 1. Возьмём, например, десятичное число 110
(в двоичной системе это число 01101110). Тогда
| Исходное число | 0110 | 1110 |
| Инверсия | 1001 | 0001 |
| Прибавляем 1 | 1001 | 0010 |
Как видим, после выполнения этих преобразований в старшем разряде у нас 1,
то есть число отрицательное. А теперь проверим, что это число действительно отрицательное.
Как это сделать? Вспомним, что (–110 + 110 = 0). То есть сложение полученных нами
двоичных чисел тоже должно дать в результате ноль. Итак
Итак
01101110 + 10010010 = 100000000
То есть у нас получилось девятиразрядное число 100000000 (десятичное 256).
Однако мы работаем с байтом, а в байте, как известно, только 8 бит (от 0 до 7).
То есть единица у нас перешла в 8-й бит, которого в байте попросту нет. То есть для
байта это эквивалентно числу 0.
В некоторых источниках дополнение до двух носит название двоичный дополнительный код.
Подведём итоги
Преобразования положительного десятичного числа со знаком в двоичное число выполняется
также как и для чисел без знака.
Преобразования отрицательного десятичного числа со знаком в отрицательное двоичное
число выполняется при помощи операции дополнение до двух (с использованием двоичного
дополнительного кода). То есть сначала число преобразовывается в двоичное,
а потом используется двоичный дополнительный код.
Преобразования положительного двоичного числа со знаком (в старшем бите 0) в десятичное
число выполняется также как и для чисел без знака.
Преобразование отрицательного двоичного числа (в старшем бите 1) в десятичное число
выполняется путём нахождения его дополнительного кода. То есть для двоичного числа 10010010
операция будет следующей:
| Исходное число | 1001 | 0010 |
| Инверсия | 0110 | 1101 |
| Прибавляем 1 | 0110 | 1110 |
В итоге получаем число 110, но поскольку в исходном числе старший бит был равен 1,
то это отрицательное число, то есть –110.
|
1. |
Положительные и отрицательные числа
|
1 |
|
2. 
|
Температура воздуха
|
1 |
|
3. |
Расположение двух чисел на координатной прямой
|
1 |
|
4. 
|
Координата точки
|
1 |
|
5. |
Название точки
|
2 |
|
6. 
|
Расстояние до нуля
|
2 |
|
7. |
Точка, симметричная данной относительно точки 0
|
2 |
|
8. 
|
Расстояние между точками на координатной прямой
|
2 |
|
9. |
Неотрицательные и неположительные числа
|
2 |
|
10. 
|
Координата точки, симметричной данной точке
|
4 |
|
11. |
Координата центра симметрии
|
4 |
|
12. 
|
Координаты трёх точек
|
3 |
«Отрицательные числа в изучении математики» (6 класс)
ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ ЧИСЛА.
История возникновения отрицательных чисел:
Впервые отрицательные числа появились в древнем Китае примерно 2100 лет тому назад. Там умели также складывать и вычитать положительные и отрицательные числа. Отрицательные числа трактовали как долг, а положительные как имущество. Таким же образом смотрели на эти числа и в Индии в VII столетии, но там уже были известны правила умножения и деления. Люди с некоторым недоверием относились к отрицательным числам, считая их не совсем реальными, истолкование их как имущество – долг вызвало недоумение: как можно «складывать» и «вычитать» имущество и долг.
Таким же образом смотрели на эти числа и в Индии в VII столетии, но там уже были известны правила умножения и деления. Люди с некоторым недоверием относились к отрицательным числам, считая их не совсем реальными, истолкование их как имущество – долг вызвало недоумение: как можно «складывать» и «вычитать» имущество и долг.
Натуральные числа принято называть положительными целыми числами. Иногда перед положительными числами ставят знак «+».
Например: + 5=5 ; +7=7.
Два положительных или два отрицательных числа-это числа одного знака. Положительное и отрицательное число-это числа разных знаков.
С помощью знака «минус» записывается число, противоположное данному:
Число противоположное а, обозначают — а
Если а=15, то -а = -15;
Если а= -20, то –а = -(-20) = 20;
Если а =0, то –а = 0. Если положительные числа появились еще в древности, и стали использоваться для счета предметов, то отрицательные числа, изобретение недавнее: Отрицательные числа возникали при вычитании. Вначале они представлялись непонятными и бессмысленными, т.к наименьшим количеством было «ничто», то есть, как всегда привыкли считать это нуль. Что может быть меньше нуля?
Если положительные числа появились еще в древности, и стали использоваться для счета предметов, то отрицательные числа, изобретение недавнее: Отрицательные числа возникали при вычитании. Вначале они представлялись непонятными и бессмысленными, т.к наименьшим количеством было «ничто», то есть, как всегда привыкли считать это нуль. Что может быть меньше нуля?
XVII веке великий французский математик Рене Декарт предложил откладывать отрицательные числа на числовой оси влево от нуля. Отрицательные числа получили реальное истолкование. Их стали признавать наравне с положительными. Наступило полное числовое равноправие.
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
О
Если перед числом стоит знак «+», его называют положительным.
Если «-», отрицательным.
Число «0» не является ни положительным , ни отрицательным.
На координатной прямой числа расположенные справа от нуля —положительные;
Числа расположенные слева от нуля — отрицательные.
Отрицательные числа.
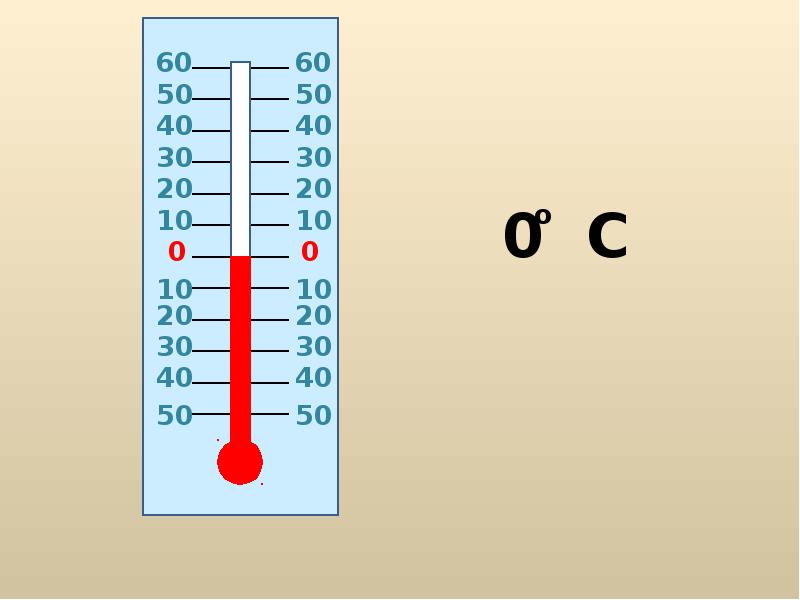
На уроках математики мы уже познакомились с натуральными , дробными числами и действиями над ними. Однако в жизни мы уже встречались и с отрицательными числами. Примером может быть обыкновенный термометр:
Из рисунка можно наблюдать, что температура может быть как выше нуля, так и ниже нуля. Со знаком «+» и со знаком «-
Любое положительное число больше нуля : 5 > 0;
Любое отрицательное число меньше нуля: — 7 < 0;
Любое отрицательное число < положительного: — 7 < 5
3.Пример применения отрицательных чисел:
— в географии:
Самая большая положительная величина на Земле –вершина
Джомолунгма +8848 м.
Самая большая отрицательная величина—
Марианская впадина — 11034 м.
-в физике:
При растяжении пружины:
Если пружину растянуть, то измерение длины является положительным числом, а если сжать –отрицательным числом.
Правила умножения положительных и отрицательных чисел:
При умножении двух чисел с разными знаками в результате получается отрицательное число, модуль которого равен произведению модулей множителей.
«+» * «-» = «-»
«-» * «+» = «-»
При умножении двух чисел с одинаковыми знаками в результате получается положительное число, модуль которого равен произведению модулей множителей.
«-» * «-» = «+»
«+» * «+» = «+»
4. Сравнение отрицательных чисел:
Сравнение отрицательных чисел:
-7 -6 -5 -4 -3 -2 -1 0 1
>
А В О
При сравнении целых отрицательных чисел, можно представить их на координатной прямой. Точка А с координатой -7 левее, чем точка В с координатой -3,
Поэтому: -7 < -3.
Из двух отрицательных чисел больше то, у которых модуль меньше.
Практические задачи:
Задача 1. Таня живет на пятом этаже многоэтажного дома, где имеется три подвала для парковки автомобилей (в лифте они указаны числами -1, -2, -3). Выйдя из своей квартиры, смогла бы Таня спуститься на лифте на семь этажей и какую кнопку ей следует нажать.
Ответ: Да, спуститься сможет. Нужно нажать на кнопку второго этажа подвала «-2»
Задача 2. Белые медведи выдерживают температуру до -800 С, моржи – выше этой температуры на 450 С, самые «морозостойкие» гуси и утки – ниже на 300 С. Какую температуру выдерживают моржи и гуси, утки?
Какую температуру выдерживают моржи и гуси, утки?
Решение: — 80 + 45 = — 350 С выдерживают моржи; — 80 – 30 = — 1100 С выдерживают гуси, утки. Ответ: — 350 С, — 1100 С.
Задание 3. Попробуйте в тексте найти положительные и отрицательные величины и сделайте выводы об их использовании в жизни.
Площадь Кунгурской Ледяной пещеры составляет 106,5 гектаров. Ее поверхность усеяна многочисленными карстовыми воронками, крупнейшие из которых достигают 50-60 метров в диаметре и 10-12 м в глубине.
В первом Бриллиантовом гроте пещеры зимой температура может достигать -15, -20 градусов, хотя в центре пещеры постоянная весна: +5 °C летом и зимой при 100% влажности.
В каменной нише Полярного грота скрывается массивная ледяная колонна, напоминающая застывший водопад. Ее еще описывал профессор М. Я. Киттара 165 лет назад.
Я. Киттара 165 лет назад.
Большое подземное озеро находится в гроте «Титанический» (площадь – 1300 кв.м., ширина 38 м, глубина достигает 3 м., температура воды постоянная +5 °C). В другом гроте – «Романтиков» экскурсанты могут любоваться небольшим озером с так называемым сифоном – подводным каналом, который опускается ниже уровня озера на 4-5 м.
(отрывок из книги Валентина Рапп «Путеводитель по Кунгуру и Ледяной пещере»)
Использованная литература:
1. Выгодский М.Я. Справочник по элементарной математике. – М.: Наука, 1972. – С. 130-136.
2. Едуш О.Ю. Математика. Подсказки на каждый день.
3. Лиман М.М. Школьникам о математике и математиках. – М.: Просвещение, 1981. – С. 26.
4. Новейший полный справочник школьника 5-11 классы. Том 1.– М.: Эксмо, 2014. – С. 224.
5. Рапп В.В. Путеводитель по Кунгуру и Ледяной пещере.– Пермь: Звезда, 1999. – С. 73-87.
6. История возникновения отрицательных чисел [Электронный ресурс]
7. История возникновения цифр. Применение отрицательных чисел.[Электронный ресурс]
История возникновения цифр. Применение отрицательных чисел.[Электронный ресурс]
Отрицательные числа (1) – Opiq
В разных странах используются различные температурные шкалы. Начиная с 1940 г., в Эстонии используется температурная шкала Цельсия. При записи к показанию температуры добавляют букву C, например, –12 °C.
При измерении температуры за начало отсчета принято считать температуру таяния льда (то же, что и температура замерзания воды). Ее обозначают 0 °C.
Когда температура ниже нуля градусов, вода замерзает, и говорят, что на улице градусы мороза. Такие показания температуры обозначают знаком минус.
Например, –5 °C.
Когда температура выше нуля, лед тает, и говорят о градусах тепла. Такие показания обозначают знаком плюс.
Такие показания обозначают знаком плюс.
Например, +3 °C.
Числа, перед которыми стоит знак –, называются отрицательными числами.
Числа, перед которыми стоит знак +, называются положительными числами.
Обычно знак плюс перед числом не пишется. Таким образом, до сих пор мы имели дело с положительными числами.
−12; −23,8; −514 – отрицательные числа.
+6; +3,25; +2212 – положительные числа.
В некоторых странах (например, в США) используется температурная шкала Фаренгейта. Эту шкалу ввел в употребление немецкий физик Даниель Габриель Фаренгейт в 1714 г.
Эту шкалу ввел в употребление немецкий физик Даниель Габриель Фаренгейт в 1714 г.
К показанию температуры прибавляется символ °F.
На шкале Фаренгейта точка таяния льда – это 32 °F, а точка кипения воды – это 212 °F. Шкала Фаренгейта и шкала Цельсия связаны следующим образом:
t °C = 59 ⋅ (t °F − 32)
До 1940 г. температурная шкала Фаренгейта использовалась и в Эстонии.
На карте прогноза погоды видно, какая была температура в различных городах Эстонии 14 марта 2012 г.
Представление положительных и отрицательных чисел в памяти компьютера. Прямой и дополнительный код числа
☰
Прямой код
Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа.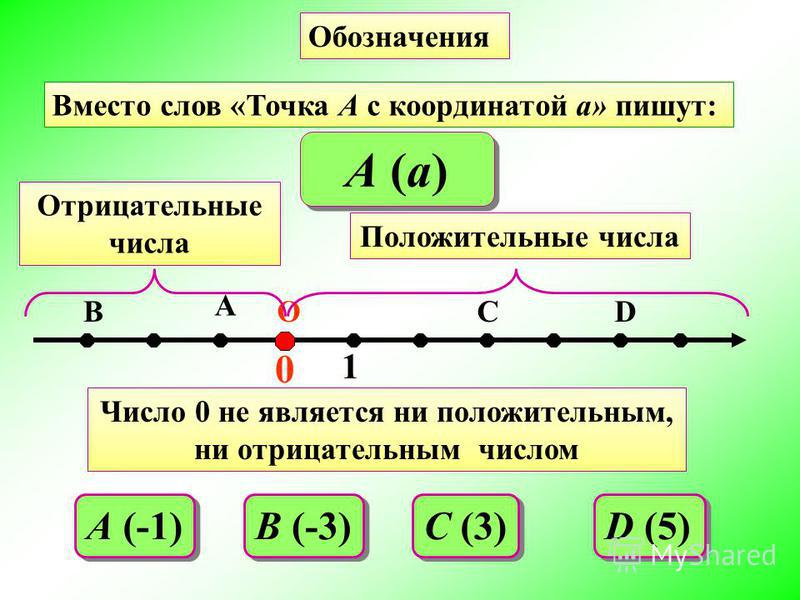 Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.
Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.
Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:
0 0001101 – положительное число
1 0001101 – отрицательное число
Количество значений, которые можно поместить в семиразрядной ячейке со знаком в дополнительном разряде равно 256. Это совпадает с количеством значений, которые можно поместить в восьмиразрядную ячейку без указания знака. Однако диапазон значений уже другой, ему принадлежат значения от -128 до 127 включительно (при переводе в десятичную систему счисления).
При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.
Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.
Дополнительный код
В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой код используется для представления положительных чисел, а дополнительный – для представления отрицательных. Поэтому, если в первом разряде находится 1, то мы имеем дело с дополнительным кодом и с отрицательным числом.
Все остальные разряды числа в дополнительном коде сначала инвертируются, т.е. заменяются противоположными (0 на 1, а 1 на 0). Например, если 1 0001100 – это прямой код числа, то при формировании его дополнительного кода, сначала надо заменить нули на единицы, а единицы на нули, кроме первого разряда. Получаем 1 1110011. Но это еще не окончательный вид дополнительного кода числа.
Далее следует прибавить единицу к получившемуся инверсией числу:
1 1110011 + 1 = 1 1110100
В итоге и получается число, которое принято называть дополнительным кодом числа.
Причина, по которой используется дополнительный код числа для представления отрицательных чисел, связана с тем, что так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.
Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.
Операция сложения положительного числа и отрицательного числа, представленного в прямом коде
- Прямой код числа 5: 0 000 0101
Прямой код числа -7: 1 000 0111 - Два исходных числа сравниваются. В разряд знака результата записывается знак большего исходного числа.
- Если числа имеют разные знаки, то вместо операции сложения используется операция вычитания из большего по модулю значения меньшего.
 При этом первый (знаковый) разряд в операции не участвует.
При этом первый (знаковый) разряд в операции не участвует._ 000 0111 000 0101 ------------- 000 0010 - После выполнения операции учитывается первый разряд. Результат операции 1 000 0010, или -210.
Операция сложения положительного числа и отрицательного числа, представленного в дополнительном коде
- Прямой код числа 5: 0 000 0101
Прямой код числа -7: 1 000 0111 - Формирование дополнительного кода числа -7.
Прямой код : 1 000 0111
Инверсия : 1 111 1000
Добавление единицы: 1 111 1001 - Операция сложения.
0 000 0101 + 1 111 1001 -------------- 1 111 1110 - Проверка результата путем преобразования к прямому коду.
Дополнительный код: 1 111 1110
Вычитание единицы : 1 111 1101
Инверсия : 1 000 0010 (или -210)
Введение в отрицательные числа | Purplemath
Purplemath
Отрицательные числа имеют долгую, а иногда и спорную историю. Математики на Индийском субконтиненте использовали отрицательные числа в течение тысячи лет, прежде чем европейцы дошли до того, чтобы принять эту идею. (Нашей системой счисления, в том числе нулем, мы обязаны индийским математикам.Раньше мы застряли в использовании римских цифр.) Китайские математики на два тысячелетия превзошли европейцев в использовании отрицательных чисел. (Юмористическое замечание: когда индейцы писали, они использовали знак «плюс», «+», для обозначения отрицательных чисел.)
Математики на Индийском субконтиненте использовали отрицательные числа в течение тысячи лет, прежде чем европейцы дошли до того, чтобы принять эту идею. (Нашей системой счисления, в том числе нулем, мы обязаны индийским математикам.Раньше мы застряли в использовании римских цифр.) Китайские математики на два тысячелетия превзошли европейцев в использовании отрицательных чисел. (Юмористическое замечание: когда индейцы писали, они использовали знак «плюс», «+», для обозначения отрицательных чисел.)
MathHelp.com
Европейцы были не единственными, кто игнорировал отрицательные числа или игнорировал их. Египтяне почти две тысячи лет назад считали отрицательные числа смешными. Европейцы, как и египтяне, использовали математику, основанную на геометрических понятиях, таких как площадь, что всегда положительно. Это замедлило их математический прогресс, потому что они бесполезно думали о числах. Однако, когда европейские ученые начали переводить арабские тексты, полученные из Северной Африки, они, наконец, познакомились с новым способом мышления и начали наверстывать упущенное.
Египтяне почти две тысячи лет назад считали отрицательные числа смешными. Европейцы, как и египтяне, использовали математику, основанную на геометрических понятиях, таких как площадь, что всегда положительно. Это замедлило их математический прогресс, потому что они бесполезно думали о числах. Однако, когда европейские ученые начали переводить арабские тексты, полученные из Северной Африки, они, наконец, познакомились с новым способом мышления и начали наверстывать упущенное.
Цель этого урока истории — объяснить, что многие поколения очень умных людей оказались неспособными принимать, не говоря уже о понимании, отрицательные числа.Так что, если у вас возникли трудности с концепцией, вы в хорошей компании. Но вы, как и эти европейцы восемнадцатого века, наконец, тоже можете это «понять»!
Когда вы впервые выучили числа еще в начальной школе, вы начали с подсчета чисел: 1, 2, 3, 4, 5, 6 и так далее. Ваша числовая строка выглядела примерно так:
Ваша числовая строка выглядела примерно так:
← проведите по экрану , чтобы просмотреть изображение полностью →
Позже вы узнали о нулях, дробях, десятичных дробях, квадратных корнях и других типах чисел, поэтому ваша числовая строка стала выглядеть примерно так:
← проведите по экрану , чтобы просмотреть изображение полностью →
Сложение, умножение и деление всегда имели смысл — до тех пор, пока вы не пытались делить на ноль, — но иногда вычитание не срабатывало.Если у вас было «9–5», вы получили 4:
.
← проведите по экрану , чтобы просмотреть изображение полностью →
… а что, если бы у вас было «5-9»? Вы просто не могли сделать это вычитание, потому что в числовой строке не хватило «места», чтобы вернуться на девять единиц:
← проведите по экрану , чтобы просмотреть изображение полностью →
Вы можете решить эту проблему с «пробелом», используя отрицательные числа. «Целые» числа начинаются с нуля и отсчитываются вправо; это положительные целые числа. Отрицательные целые числа начинаются с нуля и отсчитываются слева:
«Целые» числа начинаются с нуля и отсчитываются вправо; это положительные целые числа. Отрицательные целые числа начинаются с нуля и отсчитываются слева:
.
← проведите по экрану , чтобы просмотреть изображение полностью →
Обратите внимание на стрелку на дальнем правом конце числовой строки выше. Эта стрелка указывает направление увеличения числа. В частности, эта стрелка также говорит вам, что негативы становятся на меньше , поскольку они перемещаются влево.То есть –5 на меньше , чем –4.
Как использовать эту расширенную числовую строку? Что ж, для начала, теперь мы можем сделать вычитание «5 — 9». От нуля идем на пять единиц вправо, а затем вычитаем девять единиц слева:
← проведите по экрану , чтобы просмотреть изображение полностью →
В итоге мы получаем четыре единицы слева от нуля, так что теперь мы знаем, что 5 — 9 = –4.
Отрицательные числа сначала могут показаться немного странными, но это нормально; к негативам нужно привыкнуть.Давайте рассмотрим несколько неравенств, чтобы попрактиковаться в понимании. При необходимости обратитесь к числовой строке выше.
Заполните следующее неравенство: 3 _____ 6
Посмотрите на числовую строку выше. Поскольку 6 справа от 3, то 6 больше, поэтому правильное неравенство:
Филиал
Заполните следующее неравенство: –3 _____ 6
Посмотрите на числовую прямую (или подумайте о ней) еще раз.Каждое положительное число находится справа от каждого отрицательного числа, поэтому правильное неравенство:
Выполните следующее неравенство: –3 _____ –6
Снова подумайте о числовой прямой. Поскольку –6 находится слева от –3, то –3, находясь правее, на самом деле является большим числом. Итак, правильное неравенство:
Поскольку –6 находится слева от –3, то –3, находясь правее, на самом деле является большим числом. Итак, правильное неравенство:
Заполните следующее неравенство: 0 _____ 1
Ноль меньше любого положительного числа, поэтому:
Выполните следующее неравенство: 0 _____ –1
Ноль больше любого отрицательного числа, поэтому:
URL: https: // www.purplemath.com/modules/negative.htm
Определение отрицательного числа — определение математического слова
Определение отрицательного числа — определение математического слова — Math Open Reference
Отрицательные числа
числа меньше нуля.
Когда вы впервые сталкиваетесь с отрицательными числами, они могут сбить с толку.
Как в миске может быть меньше нуля апельсинов?
Фактически
по этой причине подсчет чисел не может быть отрицательным.Это не имеет никакого смысла.
Но когда мы используем
скалярные числа,
мы измеряем что-то вроде температуры или высоты, отрицательные значения полезны.
(См. Использование отрицательных чисел.)
Мы берем фиксированную точку и называем ее нулем. Измерения в одном направлении положительны, а в другом — отрицательны. Ноль не является ни положительным, ни отрицательным.
Попробуй это
Отрегулируйте стрелку, чтобы увидеть, как отрицательные числа лежат слева от нуля на числовой прямой. Апплет
не позволит вам установить стрелку на ноль или положительное число.
Знак ‘-‘
Отрицательные числа обозначаются знаком тире (-) впереди, например –5, –12,77.
Отрицательное число, такое как –6, произносится как «отрицательная шестерка» .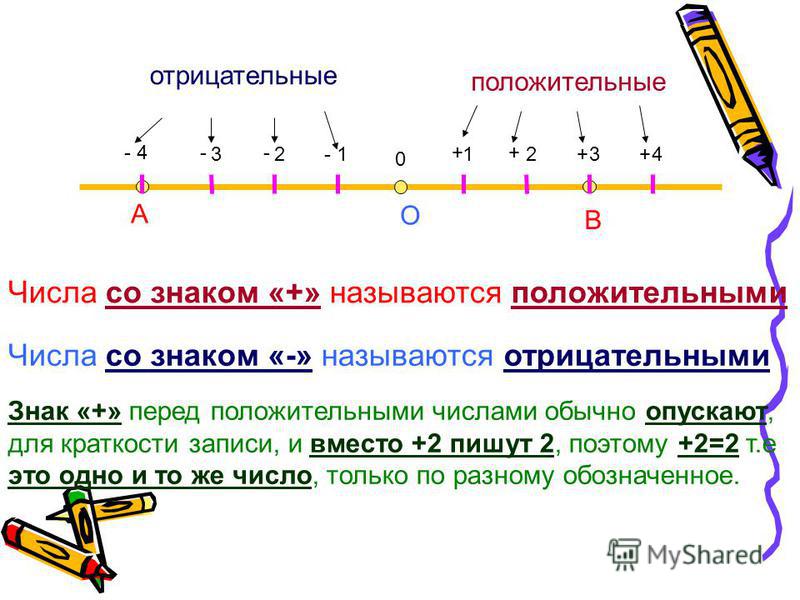
Это также означает «вычесть»
К сожалению, в математике символ «-» используется для двух разных вещей.
Оно означает отрицательное число, как описано выше, но также означает «вычесть» или «минус». Например
5–3 означает «отнимите 3 от 5» и получите результат 2.Здесь знак минус означает вычитание.
Итак, говоря об отрицательном числе, таком как –4, научитесь произносить «отрицательные четыре» , чтобы избежать путаницы.
Такая же путаница происходит со знаком плюс (& nbsp +). Видеть
Положительные числа.
См. Также Выполнение арифметических действий с положительными и отрицательными числами.
Сравнение чисел
Со всеми числами, отрицательными, нулевыми или положительными:
- Одно число больше другого, если оно находится справа от числовой строки.
- И наоборот, одно число меньше другого, когда оно находится слева в числовой строке.
Так например
- –4 меньше –1
- ноль больше -120
- 90 больше –1
Больше / меньше — будьте осторожны!
Избегайте слов «больше», «больше» и «меньше» при сравнении чисел. Они могут вас обмануть.
Они могут вас обмануть.
Например, -1000 больше -4?
Это может выглядеть так, но это не так.-1000 меньше -4, потому что он находится слева от числовой строки. Но когда вы используете слово «больше»
вы можете думать иначе. Избегайте этих двух слов в математике. Вместо этого используйте «меньше» и «больше».
Другие числовые темы
Скалярные числа
Счетные числа
Числа с делителями
Специальные значения
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Отрицательные числа и абсолютное значение — она любит математику
Этот раздел охватывает:
Отрицательные числа сначала кажутся немного пугающими, но на самом деле они не так уж и плохи.Давайте сначала повторно представим нашу числовую линию, которую я показал вам ранее:
.
Обратите внимание, что отрицательные целые числа (те, перед которыми стоит минус) находятся на том же расстоянии от нуля ( 0 ), что и положительные числа, но они находятся слева от 0 . Это все отрицательные числа; они просто идут назад так же, как и положительные числа вперед.
Это все отрицательные числа; они просто идут назад так же, как и положительные числа вперед.
Абсолютное значение числа — это расстояние от 0 , поэтому это всегда положительное число.Оно написано двумя строками вокруг числа, и это просто положительное значение того, что находится внутри строк, независимо от того, является ли число положительным или отрицательным.
В алгебре может быть немного сложнее, когда мы работаем с переменными или неизвестными, но пока вот примеры, чтобы показать, насколько действительно проста эта концепция:
\ (\ left | {-5} \ right | = 5 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , \ left | 5 \ right | = 5 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, — \ left | {-5} \ right | = -5 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ влево | 0 \ вправо | = 0 \)
Два числа называются противоположными , если они находятся на одинаковом расстоянии от 0 . Например, 2 и « –2 » — противоположности.
Например, 2 и « –2 » — противоположности.
Помните, что числа с большим абсолютным значением могут быть меньше, когда числа отрицательны, например, \ (- 6 <-5 \), а в случае дробей \ (\ displaystyle - \ frac {3} {4} <- \ frac {1} {2} \). Итак, если мы сравниваем отрицательные числа, это на самом деле обратное по сравнению с тем, к чему мы привыкли.
Давайте подумаем на примере того, как негатив может существовать в реальной жизни. Допустим, у вашей мамы есть младшая сестра, и предполагается, что ребенок родится в 5 месяцев.
Как ни странно, вашей младшей сестре –5 месяцев. В следующем месяце ей будет –4 месяцев и так далее. В день ее рождения ей 0 , и через несколько месяцев она станет позитивной. Опять же, отрицательные числа — это то же самое « расстояние » (расстояние всегда положительно) от 0 , но только в противоположном направлении. Если бы мы хотели знать, сколько времени осталось до того, как ей исполнится 9 месяцев, мы бы добавили 5 месяцев до она 0 к 9 месяцев после ей 0 , чтобы получить 14 месяцев (если задуматься, это на самом деле задача вычитания).
Если бы мы хотели знать, сколько времени осталось до того, как ей исполнится 9 месяцев, мы бы добавили 5 месяцев до она 0 к 9 месяцев после ей 0 , чтобы получить 14 месяцев (если задуматься, это на самом деле задача вычитания).
Для более сложных тем по Абсолютное значение см. Решение уравнений абсолютного значения и неравенств .
Давайте поговорим о сложении и вычитании отрицательных чисел. Для числа « –2 » это означает, что мы находимся на две позиции слева от « 0 » и на четыре позиции слева от « 2 ». Помните, что когда мы прибавляем , мы считаем до правого , а когда мы вычитаем или добавляем отрицательное число, мы считаем до слева . Таким образом, если сложить «–2 » и « 4 », мы получим « 2 ». Есть несколько правил сложения и вычитания отрицательных чисел, о которых мы скоро поговорим.
Таким образом, если сложить «–2 » и « 4 », мы получим « 2 ». Есть несколько правил сложения и вычитания отрицательных чисел, о которых мы скоро поговорим.
Теперь давайте продолжим сложение и добавим вычитание. Как уже упоминалось, сложение означает перемещение вправо , а вычитание означает перемещение влево , как показано на следующем рисунке:
Помните, что « — 3 + 5» — это то же самое, что «5 — 3», а «5 + — 6» — то же самое, что «5 — 6. »- просто запомни это !!! Также обратите внимание, что перед числом стоит знак числа, и много раз перед числами стоит невидимый знак плюса, например, когда они находятся в начале.
Итак, вот несколько правил для сложения и вычитания отрицательных чисел:
- Сложение двух положительных чисел дает положительное число.
 Например, \ (4 + 4 = 8 \).
Например, \ (4 + 4 = 8 \). - Сложение двух отрицательных чисел дает отрицательное число. Просто сложите два числа и поставьте перед ними минус. Например, \ (- 4 + -4 = -8 \). Это то же самое, что \ (- 4-4 = -8 \).
- Опять же, добавление отрицательного числа — это то же самое, что вычитание этого числа.Например, \ (\ displaystyle -4-4 = -4 + -4 \ text {} = — 8 \).
- Когда вы складываете положительное число и отрицательное число, вам нужно вычесть абсолютных значений двух чисел (большего — меньшего) и сделать знак разницы в зависимости от того, какое из них имеет наибольшее исходное число без знаков (в другими словами, наибольшее абсолютное значение). Несколько примеров:
- Для \ (- 4 + 10 \), поскольку один положительный, а другой отрицательный, вы вычтите 4 из 10 (абсолютные значения чисел) и получите 6.Теперь, поскольку \ (\ left | {10} \ right |> \ left | {-4} \ right | \) и 10 положительный, ответ будет положительным 6 .

- Для \ (- 15 + 8 \) вы должны вычесть 8 из 15 и получить 7 . Поскольку \ (\ left | {-15} \ right |> \ left | 8 \ right | \) и 15 имеет знак — перед ним, вы должны добавить «-» к 7 , чтобы получить — 7 .
- Для \ (- 4 + 10 \), поскольку один положительный, а другой отрицательный, вы вычтите 4 из 10 (абсолютные значения чисел) и получите 6.Теперь, поскольку \ (\ left | {10} \ right |> \ left | {-4} \ right | \) и 10 положительный, ответ будет положительным 6 .
- Если у вас два минуса подряд, превратите их в плюсы.Например, если у вас есть \ (4- \ left ({-8} \ right) \), это то же самое, что и \ (4 ++ \, 8 \), то есть \ (4 + 8 \), то есть 12 .
- Сложение двух положительных чисел дает положительное число.
Теперь поговорим о , умноженном на , и , делящем на отрицательные числа. На самом деле это проще, так как правил меньше:
- Умножение или деление двух положительных чисел дает положительное число. Например, \ (5 \ times 5 = 25 \).
- Умножение или деление двух отрицательных чисел дает положительное число.Например, \ (\ displaystyle -5 \ times -5 = 25 \) и \ (\ displaystyle \ frac {{- 5}} {{- 5}} = 1 \).

- Умножение или деление положительного числа на отрицательное всегда отрицательно. Например, \ (- 5 \ times 5 = -25 \).
Вот таблица, в которой все это суммируется. Интересно, как умножение на отрицательные числа проще сложения!
| Умножение и деление | Сложение и вычитание |
\ (\ begin {array} {c} \ text {Positive} \ times \, \, \ text {Positive} = \ text {Positive} \\ 4 \ times 3 = 12 \ end {array} \) | \ (\ begin {array} {c} \ text {Positive} + \, \, \ text {Positive} = \ text {Positive} \\ 4 + 4 = 8 \ end {array} \) |
\ (\ begin {array} {c} \ text {Negative} \ times \, \, \ text {Negative} = \ text {Positive} \\ — 5 \ times -5 = 25 \ end {array} \) | \ (\ begin {array} {c} \ text {Negative} + \, \, \ text {Negative} = \ text {Negative} \\ — 4 + -5 = -9 \ end {array} \) |
\ (\ begin {array} {c} \ text {Negative} \ times \, \, \ text {Positive} = \ text {Negative} \\ — 4 \ times 4 = -16 \ end {array} \) | \ (\ displaystyle \ text {Negative} + \, \, \ text {Positive} = \, \, \ text {Depends} \, \, \ text {:)} \) При сложении положительного числа и отрицательного числа нужно из вычесть абсолютных значений двух чисел (большего — меньшего) и сделать знак таким же знаком наибольшего абсолютного значения чисел: \ (- 15 + 8 = \) Вычтите 8 из 15 , чтобы получить 7 ; так как \ (\ left | {-15} \ right |> \ left | 8 \ right | \) и 15 имеет знак — перед ним, вы должны добавить «-» к 7 , чтобы получить — 7 . \ (- 8 + 15 = \) Вычтите 8 из 15 , чтобы получить 7 ; так как \ (\ left | {15} \ right |> \ left | {-8} \ right | \) и 15 положительно, вы получите 7 . ПРИМЕЧАНИЕ: Вычитание отрицательного числа — то же самое, что и сложение чисел. \ (5–10 = 5 ++ 10 = 5 + 10 = 15 \) |
Вам действительно нужно попрактиковаться с отрицательными числами, потому что вы будете часто использовать их на протяжении всей своей математической жизни; может быть, не так много в вашей «реальной» жизни, но когда вы берете уроки математики через математический анализ в старшей школе, вы все равно будете их использовать.И, как всегда, будьте осторожны с дробями!
Изучите эти правила и практикуйтесь, практикуйтесь, практикуйтесь!
Нажмите «Отправить» (стрелка справа от проблемы), чтобы решить эту проблему. Вы также можете ввести больше проблем или щелкнуть 3 точки в правом верхнем углу, чтобы просмотреть, например, проблемы.
Вы также можете ввести больше проблем или щелкнуть 3 точки в правом верхнем углу, чтобы просмотреть, например, проблемы.
Если вы нажмете «Нажмите, чтобы просмотреть шаги», вы перейдете на сайт Mathway , где вы можете зарегистрироваться для получения полной версии (шаги включены) программного обеспечения.Вы даже можете получить рабочие листы по математике.
Вы также можете перейти на сайт Mathway здесь, где вы можете зарегистрироваться, или просто использовать программное обеспечение бесплатно без подробных решений. Есть даже приложение Mathway для вашего мобильного устройства. Наслаждаться!
Далее до Степени, экспоненты, радикалы и научная нотация — вы готовы !!
Как могут существовать отрицательные числа?
Вы когда-нибудь читали градусник холодным зимним утром? Если да, возможно, вы видели отрицательное число.Во многих местах обычно зимой бывает -15 ° F или даже -20 ° F. В Антарктиде температура опускается до -128 ° F!
В Антарктиде температура опускается до -128 ° F!
Вас удивляет, как вообще возможна отрицательная температура? Как могут существовать отрицательные числа?
Вы не первый, кто задает этот вопрос! Европейские математики веками отвергали отрицательные числа. Они не думали, что отрицательные числа имеют смысл. Однако люди в Индии и Китае тысячелетиями использовали отрицательные числа. В конце концов пришли европейцы, и сегодня мы везде используем отрицательные числа.
Отрицательные числа имеют больше смысла, если мы посмотрим на числовую линию. В числовой строке все числа справа от нуля положительны. Если мы переместимся влево от нуля, они станут отрицательными:
Мы получаем отрицательное число, вычитая большее число из меньшего. Например, если мы вычтем девять из восьми, это будет выглядеть так:
8–9 = -1
Существует множество других правил использования отрицательных чисел в математике. Вы слышали, что две ошибки не делают правильных? Это может быть правдой, но два отрицательных момента делают положительный момент! Когда мы вычитаем отрицательное число, знак вычитания находится рядом с отрицательным знаком. Это означает, что мы можем заменить их знаком добавления. Вот как это выглядит, когда два негатива дают положительный результат:
Это означает, что мы можем заменить их знаком добавления. Вот как это выглядит, когда два негатива дают положительный результат:
0 — -3 = 0 + 3 = 3
Это правило также применяется при умножении. Когда мы умножаем два отрицательных числа, ответ всегда положительный:
-5 × -2 = 10
Отрицательные числа могут показаться загадочными в математических задачах. Для многих людей отрицательные числа в реальном мире имеют больше смысла. Помните то холодное утро, когда вы читали градусник? Отрицательные числа помогли понять, насколько холодна погода.Представьте термометр как числовую линию. Если термометр был в градусах Фаренгейта, то точка замерзания составляла 32 ° F. Если температура была -15 ° F, то это было 47 градусов ниже нуля. По Цельсию точка замерзания составляет 0 ° C. Это означает, что -15 ° C будет на 15 градусов ниже нуля.
Вы когда-нибудь изучали карты или географию? Если это так, возможно, вы слышали о высоте. Высота говорит нам, насколько выше или ниже уровень моря находится место.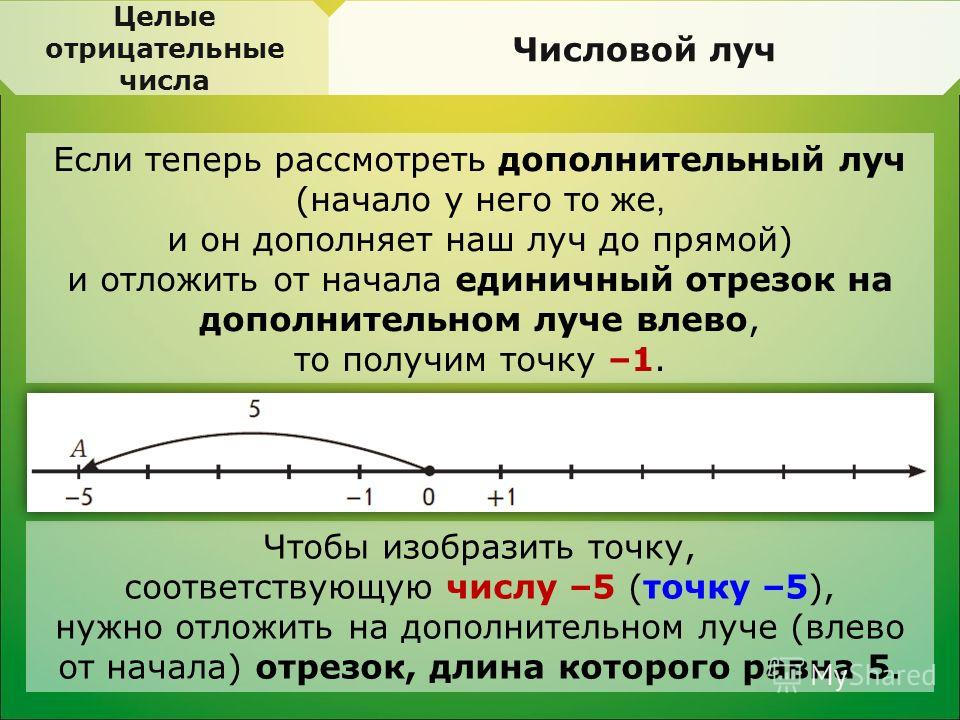 Например, пик горы Эверест находится на высоте 29 029 футов над уровнем моря.Бадуотер, Калифорния, — самая низкая точка в Соединенных Штатах. Его высота -282 фута! Это означает, что если бы бассейн Бэдуотер был ближе к океану, он был бы под водой.
Например, пик горы Эверест находится на высоте 29 029 футов над уровнем моря.Бадуотер, Калифорния, — самая низкая точка в Соединенных Штатах. Его высота -282 фута! Это означает, что если бы бассейн Бэдуотер был ближе к океану, он был бы под водой.
Еще один способ подумать об отрицательных числах — это посмотреть на банковский счет. Когда человек тратит деньги, банки используют отрицательные числа для записи транзакций. Если человек потратит 10,50 долларов на билет в кино, билет в кино будет отображаться на его или ее банковском счете как отрицательное число (-10,50). Таким образом, банк знает, что нужно вычесть 10 долларов.50 со счета.
Отрицательные числа иногда сбивают с толку, когда мы впервые узнаем о них. Правила бывает сложно запомнить! Как и все остальное, понимание отрицательных чисел становится легче с практикой. Можете ли вы придумать какие-либо другие примеры отрицательных чисел из реального мира?
отрицательных двоичных чисел | Двоичная арифметика
Поскольку сложение выполняется легко, мы можем выполнить операцию вычитания с помощью той же техники, просто сделав одно из чисел отрицательным. Например, задача вычитания 7–5 по сути такая же, как задача сложения 7 + (-5).
Например, задача вычитания 7–5 по сути такая же, как задача сложения 7 + (-5).
Поскольку мы уже знаем, как представлять положительные числа в двоичном формате, все, что нам нужно знать сейчас, это как представлять их отрицательные аналоги, и мы сможем выполнять вычитание.
Обычно мы представляем отрицательное десятичное число, помещая знак минус непосредственно слева от самой значащей цифры, как в примере выше, с -5. Однако вся цель использования двоичной записи состоит в создании схем включения / выключения, которые могут представлять битовые значения в терминах напряжения (2 альтернативных значения: «высокий» или «низкий»).
В этом контексте мы не можем позволить себе роскошь третьего символа, такого как знак «минус», поскольку эти цепи могут быть только включены или выключены (два возможных состояния). Одно из решений — зарезервировать бит (схему), который ничего не делает, кроме как представляет математический знак:
Как видите, мы должны быть осторожны, когда начинаем использовать биты для каких-либо целей, кроме стандартных значений с местами взвешивания. В противном случае 1101 2 может быть неверно истолковано как число тринадцать, когда на самом деле мы имеем в виду отрицательную пятерку.
В противном случае 1101 2 может быть неверно истолковано как число тринадцать, когда на самом деле мы имеем в виду отрицательную пятерку.
Чтобы не усложнять здесь задачу, мы должны сначала решить, сколько битов потребуется для представления наибольших чисел, с которыми мы будем иметь дело, а затем убедиться, что длина этого битового поля не превышает длины наших арифметических операций.
В приведенном выше примере я ограничился представлением чисел от отрицательной семи (1111 2 ) до положительной семи (0111 2 ) и не более, сделав четвертый бит битом «знака». Только предварительно установив эти пределы, я могу избежать путаницы отрицательного числа с большим положительным числом.
Представление отрицательной пятерки как 1101 2 является примером системы знак-величина отрицательной двоичной системы счисления. Используя крайний левый бит в качестве индикатора знака, а не взвешенного значения, я жертвую «чистой» формой двоичной записи ради чего-то, что дает мне практическое преимущество: представления отрицательных чисел.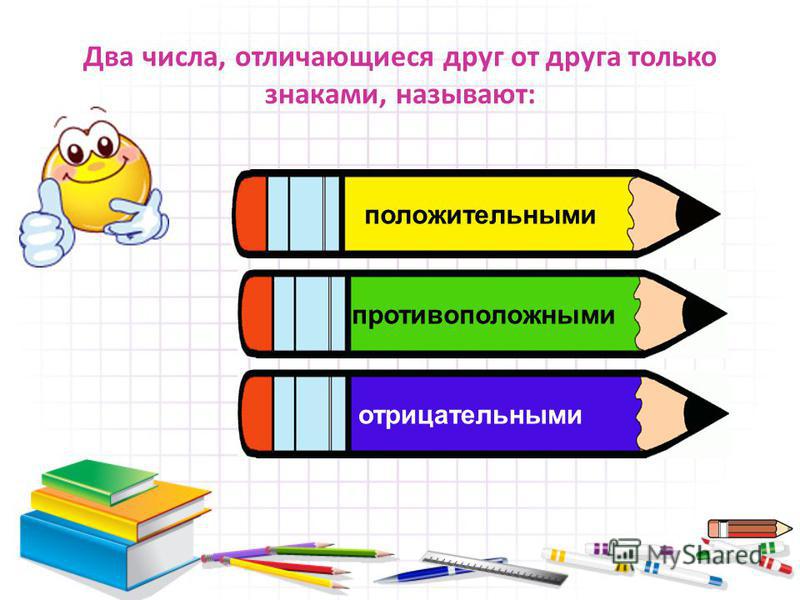
Крайний левый бит читается как знак, положительный или отрицательный, а остальные биты интерпретируются в соответствии со стандартной двоичной записью: слева направо, помещайте веса, кратные двум.
Дополнение
Каким бы простым ни был подход «знак-величина», он не очень практичен для арифметических целей. Например, как мне добавить отрицательную пятерку (1101 2 ) к любому другому числу, используя стандартную технику двоичного сложения?
Мне пришлось бы изобрести новый способ выполнения сложения, чтобы оно сработало, и если я сделаю это, то с таким же успехом я мог бы просто выполнить работу с вычитанием от руки; нет арифметических преимуществ в использовании отрицательных чисел для выполнения вычитания путем сложения, если мы должны делать это со знаковой нумерацией, и это было нашей целью!
Существует еще один метод представления отрицательных чисел, который работает с нашей знакомой техникой сложения от руки, а также имеет больше смысла с точки зрения числового взвешивания, называемого дополнением.
С помощью этой стратегии мы назначаем крайний левый бит для определенной цели, как мы это делали с подходом знак-величина, определяя наши пределы числа, как и раньше. Однако на этот раз крайний левый бит — это больше, чем просто знаковый бит; скорее, он обладает отрицательной числовой массой. Например, число отрицательных пяти будет представлено как
.
Поскольку правые три бита могут представлять величину от нуля до семи, а крайний левый бит представляет либо ноль, либо отрицательную восьмерку, мы можем успешно представить любое целое число от отрицательной семи (1001 2 = -8 10 + 1 2 = -7 10 ) до положительной семи (0111 2 = 0 10 + 7 10 = 7 10 ).
Представление положительных чисел в этой схеме (с четвертым битом, обозначенным как отрицательный вес) ничем не отличается от обычного двоичного представления. Однако представить отрицательные числа не так просто:
Обратите внимание, что отрицательные двоичные числа в правом столбце, являющиеся суммой трех правых битов плюс отрицательная восьмерка крайнего левого бита, не «считаются» в той же последовательности, что и положительные двоичные числа в левом столбце. .
.
Напротив, три правых бита должны быть установлены на правильное значение, чтобы равняться желаемой (отрицательной) сумме при суммировании с отрицательным восьмизначным значением крайнего левого бита.
Дополнение до двух
Эти три правых бита называются дополнением до двух соответствующего положительного числа. Рассмотрим следующее сравнение:
В этом случае, когда бит отрицательного веса является четвертым битом (разрядное значение отрицательной восьмерки), дополнение до двух для любого положительного числа будет любым значением, которое необходимо добавить к отрицательной восьмерке, чтобы сделать это положительное значение отрицательным эквивалентом.
К счастью, есть простой способ вычислить дополнение до двух для любого двоичного числа: просто инвертировать все биты этого числа, заменив все единицы на 0 и наоборот (чтобы получить то, что называется дополнением до единицы), а затем добавить единицу. ! Например, чтобы получить двойное дополнение до пяти (101 2 ), мы сначала инвертируем все биты, чтобы получить 010 2 («дополнение до единицы»), затем добавляем единицу, чтобы получить 011 2 , или — 5 10 в трехбитовой форме с дополнением до двух
! Например, чтобы получить двойное дополнение до пяти (101 2 ), мы сначала инвертируем все биты, чтобы получить 010 2 («дополнение до единицы»), затем добавляем единицу, чтобы получить 011 2 , или — 5 10 в трехбитовой форме с дополнением до двух
Интересно, что генерация двух дополнений двоичного числа работает одинаково, если вы манипулируете всеми битами, включая самый левый (знаковый) бит, одновременно с битами величины.Давайте попробуем это с предыдущим примером, преобразовав положительную пятерку в отрицательную пятерку, но выполнив процесс дополнения для всех четырех битов.
Мы должны обязательно включить знаковый бит 0 (положительный) в исходное число, пять (0101 2 ). Сначала инвертируем все биты для получения дополнения до единицы: 1010 2 . Затем, прибавив единицу, мы получим окончательный ответ: 1011 2 или -5 10 , выраженный в четырехбитовой форме с дополнением до двух.
Крайне важно помнить, что место бита отрицательного веса должно быть уже определено до того, как могут быть выполнены любые два преобразования с дополнением.Если бы наше поле двоичной нумерации было таким, что восьмой бит был обозначен как бит отрицательного веса (10000000 2 ), нам пришлось бы определять дополнение до двух на основе всех семи других битов.
Здесь двойное дополнение до пяти (0000101 2 ) будет 1111011 2 . Положительная пятерка в этой системе будет представлена как 00000101 2 , а отрицательная пятерка — как 11111011 2 .
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Числовая строка с отрицательными числами
Добро пожаловать на нашу страницу «Строка номеров с отрицательными числами».
Здесь вы найдете широкий спектр числовых линий для печати, содержащих положительные числа.
и отрицательные числа, которые помогут вашему ребенку понять, как работают отрицательные числа.
Вот наша подборка числовых линий для печати, включающих
положительные и отрицательные числа до 1000.
Каждая числовая строка может быть пустой или заполненной.
Использование этих листов поможет вашему ребенку:
- узнать порядок чисел в числовой строке;
- узнать, как отрицательные числа и положительные числа располагаются на числовой прямой;
- научитесь заказывать положительные и отрицательные числа.
Эти последние листы были созданы с 20 делениями, так что масштаб увеличивается в единичных единицах.
У нас также есть цветные листы и листы, которые были разработаны в качестве наглядных пособий.
Существует как книжная, так и альбомная версии большинства листов.
Мы разделили листы на разные части:
- числовые строки от -10 до 10 с увеличением единиц;
- числовые строки от -1 до 1 переходят в 0.1с;
- числовая линия увеличивается в разном масштабе.

В этом разделе каждая числовая строка идентична для каждого отдельного листа.
В этом разделе на каждом листе есть несколько числовых линий.
Взгляните на еще несколько наших рабочих листов, похожих на эти.
Вот наш выбор числовых линий от 0 до 1.
На этой странице вы найдете:
- От 0 до 10 строк стандартного и десятичного числа
- стандартные числовые линии от 0 до 1 как в книжной, так и в альбомной ориентации;
- дробь — десятичное число строк от 0 до 1.
- дробь — десятичная — процентное число строк от 0 до 1
- числовые строки от 0 до 1 с дробными полосами
Вот наша подборка бесплатных печатаемых строк с отрицательными числами только с отрицательными числами.
Использование этих листов поможет вашему ребенку:
- визуально увидеть порядок отрицательных чисел в числовой строке;
- узнать, как отрицательные числа располагаются на числовой прямой.

Вот наша подборка целочисленных строк.
Использование этих листов поможет вашему ребенку:
- узнать их числовые значения и порядок чисел;
- сравнить положение двух чисел на числовой прямой.
Номерные строки включают:
- от 0 до 10
- от 0 до 100
- 0 до 1000
- 0 до 10000
Вот наша подборка строк с десятичными числами.
Использование этих листов поможет вашему ребенку:
- узнать их числовые значения и порядок десятичных знаков;
- сравнить положение двух десятичных знаков визуально на числовой строке.
- понимает дробно-десятичный эквивалент с использованием числовых строк от 0 до 1
Вот наша подборка бесплатных печатаемых строк с дробными числами.
Использование этих листов поможет вашему ребенку:
- см. Визуально порядок дробей в числовой строке;
- число, кратное целому ряду дробей;
- видеть, когда две дроби эквивалентны;
- Разместите дроби на числовой прямой.

Использование этих листов поможет вашему ребенку:
- научиться позиционировать числа в правильном положении в строке;
- научиться считать вперед и назад с шагом разного размера.
Пустые листы с числовыми строками рассчитаны на от 2 до 11 делений.
Эти рабочие листы по математике для первого класса дадут вашему ребенку хорошее представление о разрядах и числовых последовательностях до 100.
Использование этих листов поможет вашему ребенку:
- рассчитывать и возвращать по одному;
- номер позиции до 100 в числовой строке.
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике.
и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
Могут ли отрицательные числа быть простыми?
Ответ первый: №
Согласно обычному определению простых чисел для целых чисел, отрицательные числа не могут быть простыми.
Согласно этому определению, простые числа — это целые числа больше единицы, не имеющие положительного
делители помимо одного и самого себя. Отрицательные числа исключены. По факту,
о них не думают.
Ответ второй: Да.
Теперь предположим, что мы хотим ввести отрицательные числа: тогда — a
делит b , когда каждые a делит, поэтому мы рассматриваем их как по существу
тот же делитель .Это происходит потому, что -1 делит 1, что
в свою очередь все разделяет.
Числа, которые делят единицу, называются единицами . Два числа и
и b , для которого a является единицей, умноженной на b , называются ассоциатами .
Таким образом, указанные выше делители a и — a из b являются ассоциированными.
Таким же образом -3 и 3 являются ассоциированными, и в некотором смысле представляют
то же простое .
Так что да, отрицательные целые числа могут быть простыми (если смотреть с этой точки зрения). В
на самом деле целое число — p простое всякий раз, когда p , но поскольку они
единомышленники, у нас действительно нет новых простых чисел. Проиллюстрируем
это с другим примером.
Целые числа Гаусса — это комплексные числа a + b i
где a и b — оба целые числа.(Здесь i —
квадратный корень из -1). Всего четыре единицы (целые числа,
разделите единицу) в этой системе счисления: 1, -1, i и — i . Так
у каждого простого числа есть четыре партнера.
Можно создать систему, в которой каждое простое число имеет бесконечно
много единомышленников.
Ответ третий: Неважно
В более общих числовых полях вышеуказанная путаница исчезает.Что
потому что большинство этих полей не являются главными идеальными областями и простыми числами
тогда они представлены идеалами, а не отдельными элементами.

 То есть, если стоят рядом два минуса, в сумме получается плюс.
То есть, если стоят рядом два минуса, в сумме получается плюс. При этом первый (знаковый) разряд в операции не участвует.
При этом первый (знаковый) разряд в операции не участвует.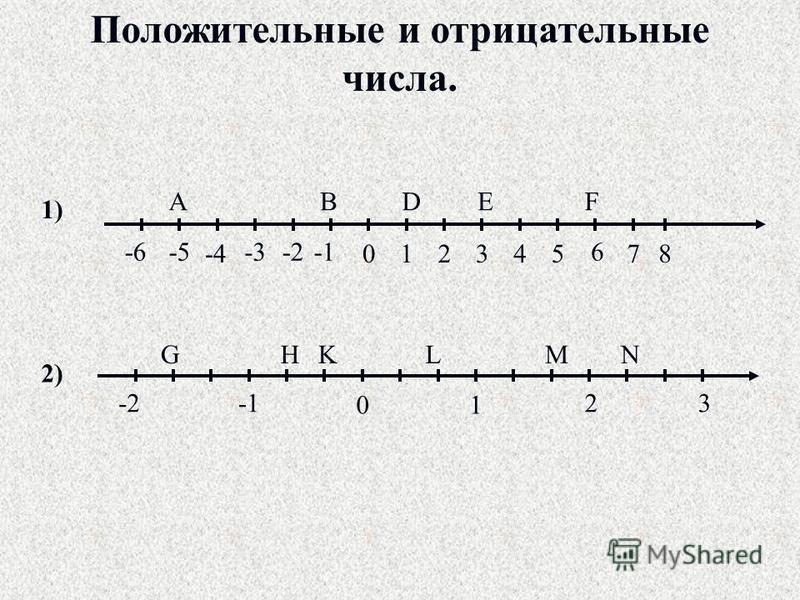 Например, \ (4 + 4 = 8 \).
Например, \ (4 + 4 = 8 \).